Курсовая работа: Анализ электрического состояния линейных электрических цепей постоянного тока

I7-I1-I2-I4=0; I7-I1-I2-I4=0;

E2-E1=R3I3-(R5+r01) I5+(R6+r02) I6; 10=53I6-46I5+22I3;

E1=R2I2+(R5+r01) I5+R7I7; 0=55I7+27I2+46I5;

0=R4I4-R3I3-R2I2; 0=33I4-22I3-27I2;

0=I1R1-I4R4; 0=16I1-33I4;

Решив данную систему, мы найдем истинные токи в ветвях.

1.2 Определяем токи во всех ветвях схемы на основе метода контурных токов

Преобразуем схему (рис.1.0) в эквивалентную (рис.1.1):

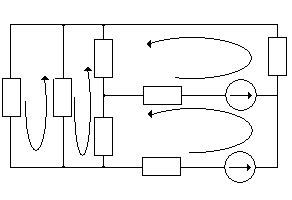
IK3 IK2

IK4 R2 R5 E2,r02 R7

R1 R4

IK1

R3 R6

E1,r01

Рис.1.1

Составляем уравнения для 4-х. контуров:

I-й. Контур:

E2-E1=IK1(R6+r02+r01+R5+R3) +IK2(R5+r01) - IK3R3;

II-й. Контур:

E1= IK2(R5+r01+R7+R2) +IK3R2-IK1(R5+r01);

III-й. Контур:

0=IK3(R4+R3+R2) - IK2R2-IK1R3-IK4R4;

IV-й. Контур:

0=IK4(R1+R4) - IK3R4;

Решаем систему:

10=121IK1-46IK2-22IK2;

30=128IK2-27IK3-46IK1;

0=82IK3-27IK2-22IK1-33IK4;

0=49IK4-33IK3;

49IK4-33IK3 => 49IK4=33IK3 => IK4=0,67347IK3;