Курсовая работа: Анализ на чувствительность двойственных оценок
Симплексный метод решения задач линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет опорный план, и когда ее опорный план является невырожденным, причем, целевая функция исследуется на максимум).
Указанный переход возможен, если известен какой-либо исходный план. Рассмотрим задачу (1.1) - (1.4), где
;
;
;…; 
; 
;…;
; 
.
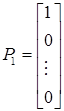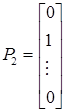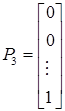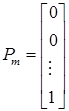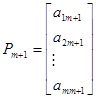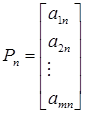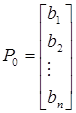Так как
,
то опорный план согласно признаку оптимальности будет иметь вид:
В опорном плане присутствует (n-m) – нулей. Этот план определяется системой единичных векторов P1 ,…,Pm , которые образуют базис m- мерного пространства, следовательно, некоторые из векторов 
могут быть представлены в виде линейной комбинации векторов данного базиса. Пусть
.
Положим
; 
.
Так как P1 ,…,Pm являются единичными векторами, то 
и
а 
, (1.5)
где Δj – критерий остановки, j=
.
В симплекс методе все решения связанные с определением оптимальности и выявлением целесообразности перехода к новому опорному плану принимаются в соответствии с ниже приведенными теоремами.
Теорема 1. (Признак оптимальности опорного плана) Опорный план
для задач (1.3), (1.4) является оптимальным, если все оценки
.
Теорема 2. (Признак неограниченности сверху) Если 
для некоторого 
и среди чисел 
нет положительных (
), то задачи (3), (4) являются неограниченными сверху на множестве плана.
Сформулированные теоремы позволяют проверить, является ли найденный опорный план оптимальным, и выявить целесообразность перехода к новому плану.
Исследование опорного плана на оптимальность, а также дальнейший вычислительный процесс удобнее вести, если условия задачи и первоначальные данные, полученные после определения исходного опорного плана, записать в симплексную таблицу (таблица 1).
Таблица 1
Симплексная таблица
| i | базис | Cбаз | P0 | С1 | С2 | … | Cr | … | Сm | Cm +1 | … | Ck | … | Cn |
| P1 | P2 | … | Pr | … | Pm | Pm +1 | … | Pk | … | Pn | ||||
| 1 | P1 | C1 | b1 | 1 | 0 | … | 0 | … | 0 | a1 m +1 | … | a1 k | … | a1n |
| 2 | P2 | C2 | b2 | 0 | 1 | … | 0 | … | 0 | a2m+1 | … | a2k | … | a2n |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| r | Pr | Cr | br | 0 | 0 | … | 1 | … | 0 | arm+1 | … | ark | … | arn |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| m | Pm | Cm | bm | 0 | 0 | … | 0 | … | 1 | amm+1 | … | amk | … | amn |
| m+1 | F0 | D1 | D2 | … | Dr | … | Dm | Dm+1 | … | Dk | … | Dn |
В столбце Cбаз записываются коэффициенты при неизвестных целевой функции, имеющие те же индексы, что и векторы данного базиса.
В столбце P0 записываются положительные компоненты искомого опорного плана. В нем же в результате вычислений записываются компоненты опорного плана. Столбцы векторов Pj представляют собой коэффициенты разложения по векторам данного базиса.
В таблице 1.1 первые m строк определяются исходными данными задачи, а показатели (m+1)-ой строки вычисляют. В этой строке в столбце вектора P0 записывается значение целевой функции, которое она принимает при данном опорном плане, а в столбце вектора Pj – значение
.
Значение F0 равно скалярному произведению вектора Р0 на вектор сбаз :