Курсовая работа: Анализ на чувствительность двойственных оценок

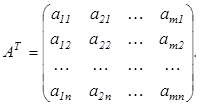
Число переменных в двойственной задаче (1.11)–(1.13) равно числу соотношений в системе (1.9) исходной задачи (1.8)–(1.10), а число ограничений в системе (1.12) двойственной задачи–числу переменных в исходной задаче.

Коэффициентами при неизвестных в целевой функции (1.11) двойственной задачи (1.11)–(1.13) являются свободные члены в системе (1.9) исходной задачи (1.8)–(1.10) а правыми частями в соотношениях системы (1.12) двойственной задачи – коэффициенты при неизвестных в целевой функции (1.8) исходной задачи.

Если переменная , исходной задачи (1.8)–(1.10) может принимать только лишь положительные значения, то j-е условие в системе (1.12) двойственной задачи (1.11)–(1.13) является неравенством вида «». Если же переменная может принимать как положительные, так и отрицательные значения, то j-е соотношение в системе (1.12) представляет собой уравнение. Аналогичные связи имеют место между ограничениями (7.2) исходной задачи (1.8)–(1.10) и переменными двойственной задачи (1.11)–(1.13) , т.е. если i-е соотношение в системе (1.9) исходной задачи является неравенством, то i-я переменная двойственной задачи . В противном случае переменная может принимать как положительные, так и отрицательные значения.

1.2.2 Правила анализа на чувствительность двойственной оценки

Всякое изменение исходных данных прямой задачи может оказать влияние, как на ее оптимальный план, так и на систему оптимальных двойственных оценок. Поэтому, чтобы проводить экономический анализ с использованием двойственных оценок, нужно знать их интервал устойчивости.

Рассмотрим пару двойственных задач.

Исходная задача: найти максимум функции

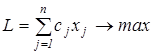(7.7)

при условиях

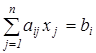
(7.8)

(7.9)

Двойственная задача: найти минимум функции

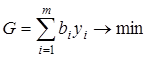(7.10)

при условиях

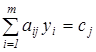
(7.11)

Предположим, что задача (7.7)–(7.9) имеет невырожденные опорные планы и хотя бы один из них является оптимальным.

Максимальное значение целевой функции (7.7) задачи (7.7)–(7.9) будем рассматривать как функцию свободных членов системы линейных уравнений (7.8): .

Теорема. В оптимальном плане двойственной задачи (7.10), (7.11) значение переменной численно равно частной производной функции по данному аргументу, т. е.

(7.12)

Последнее равенство означает, что изменение значений величин приводит к увеличению или уменьшению . Это изменение определяется величиной и может быть охарактеризовано лишь тогда, когда при изменении величин значения переменных в оптимальном плане соответствующей двойственной задачи (7.10), (7.11) остаются неизменными. Поэтому представляет интерес определить такие интервалы изменения каждого из свободных членов системы линейных уравнений. (7.8), в которых оптимальный план двойственной задачи (7.10), (7.11) не меняется. Это имеет место для всех тех значений , при которых столбец вектора последней симплекс-таблицы решения задачи (7.7)–(7.9) не содержит отрицательных чисел, т. е. тогда, когда среди компонент вектора нет отрицательных. Здесь — матрица, обратная матрице В, составленной из компонент векторов базиса, который определяет оптимальный план задачи (7.7)–(7.9).

Таким образом, если найдено решение задачи (7.7)–(7.9), то нетрудно провести анализ устойчивости двойственных оценок относительно изменений . Это, в свою очередь, позволяет:

1. проанализировать устойчивость оптимального плана задачи (7.10), (7.11) относительно изменений свободных членов системы линейных уравнений (7.8),

2. оценить степень влияния изменения , на максимальное значение целевой функции задачи (7.7)–(7.9), что дает возможность определить наиболее целесообразный вариант возможных изменений .

Вывод

В теоретической части пояснительной записки к курсовой работе приведен краткий теоретический материал о формах представления задач линейного программирование, симплексный метод и метод двойственной задачи, необходимый для решения задач линейного программирования.

линейный симплекс программирование двойственный

2. Практическая часть