Курсовая работа: Анализ на чувствительность двойственных оценок

После заполнения таблицы (1.1) исходный опорный план проверяют на оптимальность. Для этого просматривают элементы (m+1) – ой строки таблицы. В результате может иметь место один из следующих трех случаев:

1) Значения Δ_j больше или равны нулю для всех ;

2) Δ_j <0 для некоторого j и все соответствующие этому индексу величиныa_ij <0 для ;

3) Δ_j <0 для некоторых индексов j, и для каждого такого j по крайней мере одно из чисел a_ij >0.

В первом случае на основании признака оптимальности исходный опорный план является оптимальным. Во втором случае целевая функция не ограничена сверху на множестве планов, а в третьем случае можно перейти от исходного плана к новому опорному плану, при котором значение целевой функции увеличится. Этот переход от нового опорного плана к другому осуществляется исключением из исходного базиса какого-нибудь из векторов и введением в него нового вектора, исходя из максимальной абсолютной величины отрицательных чисел Δ_j . Если таких чисел несколько, то в базис вводится вектор, имеющий тот же индекс, что и максимум из чисел c_j , где Δ_j <0.

Пусть , остальные Δ_j ³ 0, следовательно, в базис вводится вектор P_k . Для того чтобы определить вектор, подлежащий исключению из базиса, находим минимальное значение отношения: .

Пусть это достигается для некоторого i=r. Тогда из базиса исключается вектор Р_r , а число a_rk называют разрешающим (генеральным) элементом. Столбец и строку, на пересечении которых находится элемент a_rk называют направляющими (генеральными).

После выделения направляющей строки и направляющего столбца находят новый опорный план и коэффициенты разложения векторов Р_j через векторы нового базиса, соответствующего новому опорному плану. Положительные компоненты нового опорного плана вычисляются по формулам:

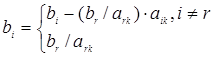(1.6)

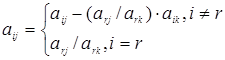(1.7)

После вычисления a_ij иb_i согласно формулам (1.6) и (1.7) их значения заносят в новую таблицу. Элементы (m+1)-ой строки вычисляются на основе их определения. После заполнения новой симплекс-таблицы просматривают элементы (m+1)-ой строки. Если все ≥0, то новый опорный план является оптимальным. Если же среди указанных чисел имеются отрицательные, то, используя описанную выше последовательность действий, находят новый опорный план. Этот процесс продолжают до тех пор, пока либо не получают оптимальный план задачи, либо не устанавливают ее неразрешимость

1.2 Двойственная задача линейного программирования

Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной по отношению к исходной (прямой) задаче.

Рассмотрим следующую задачу линейного программирования.

(1.8)

при условиях

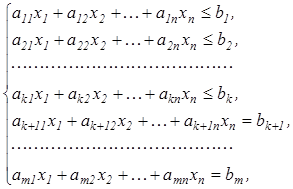(1.9)

(1.10)

Определение. Задача, состоящая в нахождении минимального значения функции

(1.11)

при условиях

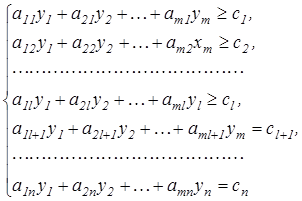(1.12)

(1.13)

называется двойственной по отношению к задаче (1.8)–(1.10).

Задачи (1.8)–(1.10) и (1.11)–(1.13) образуют пару задач, называемую в линейном программировании двойственной парой.

1.2.1 Правила составления двойственной задачи

Двойственная задача по отношению к исходной составляется согласно следующим правилам:

Целевая функция исходной задачи (1.8)–(1.10) исследуется на максимум, а целевая функция двойственной (1.11)–(1.13) –на минимум.