Курсовая работа: Анализ системы управления Общежитие

Ректорат

Директор студгородка

Договоры

Заявления, справки

Подсистема 11 - Касса Прием платежей, передача платежных поручений Проживающие Квитанции Внешняя сущность 12 – Технический персонал Уборка общежития, проведение ремонтных работ

комендант

Заявления Подсистема 13- Банк

Начисление и выдача заработной платы

Начисление и выдача стипендий и платежи за проживание

Комендант

Чеки, квитанции

Чеки, квитанции

Внешняя сущность 14 – Пожарная служба Контроль за состоянием противопожарной системы, установка сигнализации

Комендант

Инструкции

Внешняя сущность 15 – Медицинско-санитарная служба Контроль за содержанием санитарных условий

Комендант

Инструкции

Внешняя сущность

2. Представление структуры управления в виде графа

Для моделирования структур СУ удобно использовать графы. Графом системы управления (ГСУ) называется граф G=G(X,U), в котором множество вершин X интерпретирует множество элементов СУ, а множество ребер U — множество связей между ними. Важным преимуществом модели в виде ГСУ является возможность эффективного применения компьютерных технологий для автоматизации обнаружения критических структурных свойств исследуемой СУ.

Граф имеет следующие основные формы представления:

- графический (в виде диаграммы);

- матричный;

- теоретико-множественный;

- в виде списка.

В данной курсовой работе используется два первых способа представления графа. Система управления «Общежитие» в виде диаграммы графа представлена на рисунке 2.1.

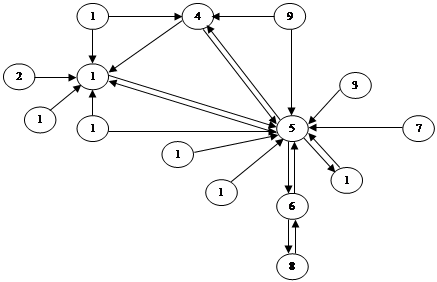
Рисунок 2.1 –Диаграмма графа системы управления «Общежитие»

Диаграмма графа иллюстрирует множество точек, расположенных на плоскости и интерпретирующих вершины графа, и множество жордановых дуг, соединяющих эти точки и интерпретирующих ребра графа. Граф построен в соответствии с данными таблицы 1.1. Вершины графа на диаграмме изображены как окружности с номерами внутри. Нумерация вершин графа совпадает с нумерацией элементов СУ из таблицы 1.1.

Далее рассмотрим второй способ представления графа – матричный. Основными матрицами графа являются матрицы смежностей, инциденций и матрица основных контуров.

2.1 Матрица смежностей

Матрицей смежностей орграфа, имеющего n вершин, называется матрица A=||||n´n, элемент которой =1, если вершина i смежна к вершине j (т.е. дуга направлена от вершины i к вершине j) и =0 в противном случае. Матрица смежностей ГСУ «Общежитие» представлена на рисунке 2.2.

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	ρ+
1	1	1	2
2	1	1
3	1	1
4	1	1	2
5	1	1	1	1	4
6	1	1	2
7	1	1
8	1	1
9	1	1	2
10	1	1
11	1	1
12	1	1
13	1	1	2
14	1	1
15	1	1
ρ-	0	0	0	3	10	2	0	1	0	6	0	1	0	0	0

Рисунок 2.2 – Матрица смежностей A

Из данной матрицы можно увидеть, что сумма всех элементов матрицы равна числу дуг орграфа. Сумма элементов строки i равна полустепени исхода вершины i, а сумма элементов столбца j равна полустепени захода вершины j.

2.2 Матрица инциденций

Матрицей инциденций орграфа, имеющего n вершин и m дуг, называется матрица B=||||_{n ´ m} , у которой =1, если дуга j инцидентна вершине i и направлена от нее, = -1, если дуга j инцидентна вершине i и направлена к ней, и =0 в противном случае. На рисунке 2.3 представлена матрица инциденций ГСУ «Общежитие».

1/4	1/10	2/10	3/5	4/5	4/10	5/4	5/6	5/10	5/12	6/5	6/8	7/5	8/6	9/4	9/5	10/5	11/10	12/5	13/5	13/10	14/5	15/5
1	1	1
2	1
3	1
4	-1	1	1	-1	-1
5	-1	-1	1	1	1	1	-1	-1	-1	-1	-1	-1	-1	-1
6	-1	1	1	-1
7	1
8	-1	1
9	1	1
10	-1	-1	-1	-1	1	-1	-1
11	1
12	-1	1
13	1	1
14	1
15	1

Рисунок 2.3 – Матрица инциденций B

2.3 Матрица основных контуров