Курсовая работа: Автоколебательная система. Волны пластической деформации

где проведем линеаризацию, т.е. опустим все нелинейные слагаемые по малым смещениям и . В результате получим

(2.20)

(2.21)

В итоге ляпуновские показатели для точки S будут следующими:

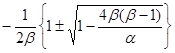=. (2.22)

Проведем анализ полученных результатов. С учетом того, что в формуле (2.22) присутствует радикал то можно сделать вывод, что при значениях параметра, ограниченных сверху величиной

=, (2.23)

ляпуновские показатели вещественны и отрицательны а с ростом до значений превышающих критическое, они становятся комплексными с отрицательной действительной частью. Следовательно, в этих пределах точка F представляет устойчивые узел и фокус соответственно.

Можно сделать вывод, что системы, в которых предпочтителен колебательный режим реализуются, если интенсивность процессов аннигиляции жертвы мала по сравнению с интенсивностью процесса ее поглощения хищником. С другой стороны, характерное время автономной эволюции хищника должно быть малым в сравнении с соответствующим временем для жертвы.

2.1.5 Построение фазовых портретов

Для построения фазовых портретов были использованы слабый численный метод Рунге-Кутта 4 порядка точности. Среда реализации – математический пакет Matlab. Для получения данных, численно интегрировалась обезразмеренная система дифференциальных уравнений (2.3), (2.4). Полученные результаты изображены на рис. 2.1-2.2.

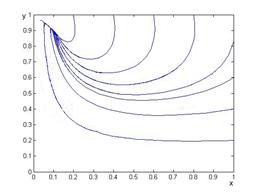
Рисунок 2.1. — Фазовый портрет системы «Хищник-жертва»: режим регрессии.

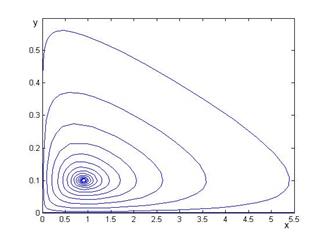
Рисунок 2.2. — Фазовый портрет системы «Хищник-жертва»: режим регрессии.

2.2 Волны пластической деформации

2.2.1 Постановка задачи

Необходимо получить уравнение с безразмерными величинами, определить координаты особых точек. Найти показатели Ляпунова для особых точек, определить характер их устойчивости. Построить фазовые портреты системы.

2.2.2 Получение уравнений с обезразмеренными величинами.

Исследуемая система уравнений имеют вид

(2.24)

(2.25)

Введем безразмерное напряжение , время , а также параметры , , >1. Тогда система уравнений (2.1), (2.2) принимает вид

(2.26)

. (2.27)

Здесь все величины не имеют размерностей, следовательно, система была вполне успешно обезразмерена.

2.2.3 Определение координат особых точек

Поскольку аналитически получить точные зависимости из системы нелинейных дифференциальных уравнений (2.26), (2.27) не представляется возможным, проведем ее качественное исследование методом фазовой плоскости. Такой анализ дает возможность определить характер фазовых траекторий, совокупность которых с различными начальными координатами определяет фазовый портрет системы. Точный его вид найдем путем численного интегрирования системы уравнений (2.26), (2.27).

Разделив почленно уравнение (2.26) на (2.27), получаем дифференциальное уравнений первой степени

. (2.28)