Курсовая работа: Автоматическая система регулирования температуры
Рис.5. Статическая характеристика нелинейности F3(u)
2.1.4. F 4( u н) – нелинейная зависимость мощности электротеплового преобразователя (нагревателя) от напряжения;
![]()
P н – мощность;
Rн – активное сопротивление нагревателя;
C – теплоемкость печи;
γ – коэффициент, моделирующий тепловое сопротивление теплоизоляции;
θ – температура;
θс- температура окружающей среды;
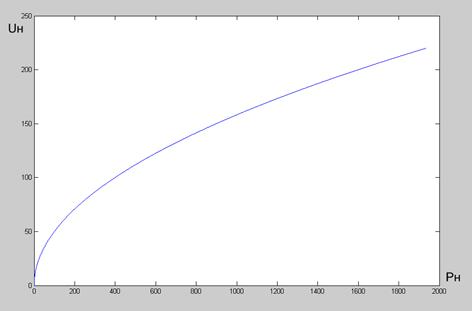
Рис. 6. Статическая характеристика нелинейности F4(u)
2.2 Линеаризация системы в рабочей точке
В нормально функционирующей САУ значение регулируемой и всех промежуточных величин незначительно отличается от требуемых. В пределах малых отклонений все нелинейные зависимости между величинами, входящими уравнение динамики, могут быть приближенно представлены отрезками прямых линий.
Для линеаризации системы воспользуемся общей статической характеристикой всех нелинейностей, а именно зависимостью мощности нагревателя от напряжения управления (нелинейностью типа Ограничение можно пренебречь, так как предполагается работа системы в рабочей точке). С помощью расчетов были установлены значения всех величин в рабочей точке системы, для данной зависимости это будут Pн=275 Дж и Up=1.046 В.
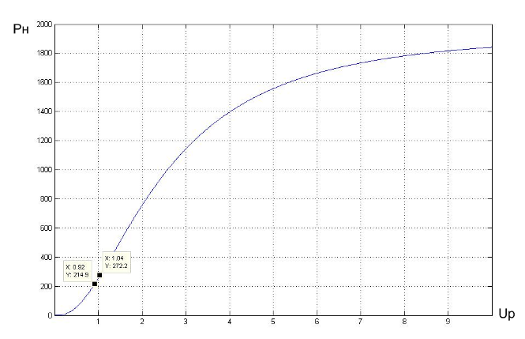
Суть линеаризации состоит в том, чтобы заменить нелинейную характеристику блоков системы прямой линией в окрестностях рабочей точки. Предполагая работу системы при малых отклонениях, можно пренебречь постоянной составляющей и заменить нелинейность линией типа y=k*x.
Т.к. для нашего случаю рабочая точка находится на линейном участке для линеаризации достаточно выбрать две координаты возле рабочей точки и найти уравнение прямой, проходящей через эти две точки. В итоге получаем Pн=476.19*Up.
Изобразим линию в одной системе координат с нелинейной характеристикой:
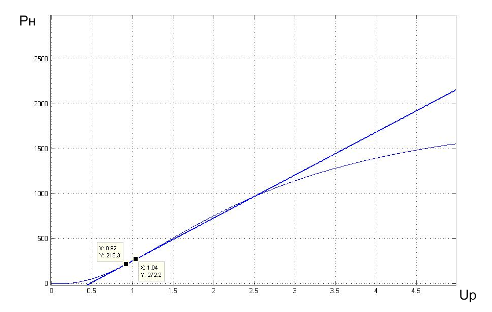
Таким образом мы заменяем нелинейные блоки системы F2, F3, F4 одним пропорциональным звеном с K=476.19. Таким образом структурная схема системы существенно упростилась:
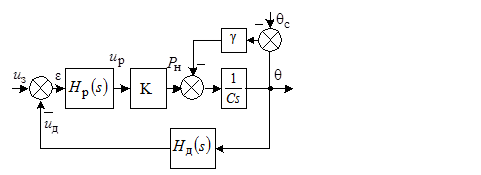
2.3 Передаточные функции линеаризованной системы
2.3.1 П.ф. разомкнутой системы по выходной переменной относительно сигнала:
![]()
2.3.2. П.ф. замкнутой системы по выходной переменной относительно задающего и возмущающего воздействий:
![]() ;
;
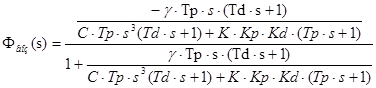 ;
;
2.4 Характеристическое уравнение системы:
![]()
Характеристический полином:
![]()
![]()