Курсовая работа: Численные характеристики дискретных случайных величин

где совместная плотность случайных величин

За характеристику зависимости между двумя случайными величинами и принимается отношение их ковариации к произведению их средних квадратических отклонений. Эта безразмерная величина называется коэффициентом корреляции величин и :

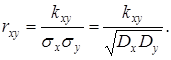
Таким образом, чтобы получить числовые характеристики двумерного случайного вектора, следует добавить к математическим ожиданиям и дисперсиям его координат еще и ковариацию или коэффициент корреляции.

Очевидно, что ковариация случайной величины с сама с собой равно ее дисперсии, а ее коэффициент корреляции с самой собой равен единице, и в более общем случае, когда

Коррелированные и некоррелированные случайные величины

Зависимость между случайными величинами, характеризуемая коэффициентом корреляции, называется, корреляцией. Случайные величины называются коррелированными, если их коэффициент корреляции равен нулю. Из формулы 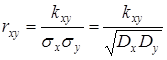следует, что случайные величины не коррелированны тогда и только тогда, когда их ковариация равна нулю.

Легко видеть, что для некоррелированности случайных величин достаточно, чтобы их совместное распределение было симметрично относительно какой-нибудь прямой, параллельной одной из осей координат.

Моменты первого и второго порядков случайной величины

Математическое ожидание, дисперсия и ковариация представляют собой частные виды моментов случайных причин.

Моментом первого порядка (первым моментом) случайной величины называется ее математическое ожидание.

Моментом второго порядка (вторым моментом) скалярной (в общем случае комплексной) случайной величины называется математическое ожидание квадрата ее модуля:

Центральным моментом второго порядка величины называется момент второго порядка центрированной величины т.е. ее дисперсия.

Моментом второго порядка величины относительно точки называется момент второго порядка разности

(*)

Очевидно, что

Смешанным моментом второго порядка скалярных случайных величин и называется математическое ожидание произведения первой величины и сопряженной второй:

Центральным смешанным моментом второго порядка величин и называется смешанный второй момент центрированных случайных величин и , т.е. ковариация величин и .

Смешанным моментом второго порядка величин и относительно точек и называется смешанный второй момент разностей и

(**)

Ясно, что

Подставив в и и пользуясь свойствами математических ожиданий, получим выражения моментов второго порядка через математические ожидания и центральные моменты второго порядка:

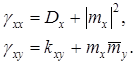
Аналогично из (*) и (**) получаем