Курсовая работа: Деякі скінченно-різнецеві методи розвязування звичайних диференціальних рівнянь

LET anew = f(x) І значення на (п+1) -му кроці LET v = v + (2*anew + 5*a - aold)*dt/6

LET aold = a значення на (n-1) -му кроці

LET а = anew значення на n-му кроці END SUB

DEF f(x) LET e = exp(- x) LET f = 2*e*(e - 1) END DEF

SUB energY(x, v, ecum, e2cuin) LET KE = 0.5*v" v LET e = exp(- x) LET PE = e*{e - 2) LET etot = KE + PE LET ecum = ecum + etot LET e2cum = e2cum + etot*etot END SUB

SUB output{ecum, e2cuiT!, n) LET n = n + 1 І вирахування початкового значення

LET ebar = ecum/n PRINT "середня енергія = ";ebar LET sigma2 = e2cum/n - ebar*ebar PRINT "sigma = "; sqr(sigma2) END SUB

Метод Адамса

Цей метод чисельного інтегрування розроблений Адамсом в 1855 році на прохання видомого англійського алтелериста Башфора, який займався внутрішньою балістикою. В подальшому цей метод був забутий і знову відкритий був норвезьким математиком Штермером. Популяризація метода Адамса і подальше його вдосконалення пов’язане із іменем Крилова.

Запишемо рівняння першого порядку

З початковими умовами 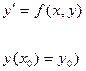(1,2)

Нехай x_i ( i =0,1,2…)- система рівнозначних значень з кроком h i y(x_i ). Очевидно маємо

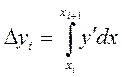(3)

В силу другої інтерполяційної формули Ньютона з точністб до різниць четвертого порядку отримуємо:

(4)

де або (4а)

Підставляю вираз (4а) в формулу (3) і враховуючи те, що будемо мати

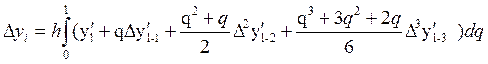
З відси отримуємо формулу експоляриціональну Адамса

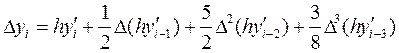(5)

Для початкового процессу потрібно чотири початкових значення y_0, y_1, y₂ , y_3, - початковий відрізок, який приділяє, виходячи із початкових умов (2), яким-небуть чисельним методом. Мажна наприклад використати метод Рунге-Кутта або розкласти в ряд Тейлора

Де i =1,2,3 (або i =-1,1,2) із відповідною зміною нумерування. Знаючи ці значення, із рівнянь (1) можна знайти значення похідних і скласти таблицю

(6)

Подальше значення y_i ( i =4,5…) шуканого розвязку можна крок за кроком обчислювати за формулою Адамса, поповнюючи по мірі можливості таблицю різниць (6)

Вирахувавши перше наближення для по формулі

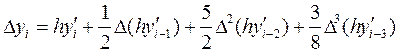
Визначити підрахувати кінцеві різниці

(7)