Курсовая работа: Деякі скінченно-різнецеві методи розвязування звичайних диференціальних рівнянь
(8)
Якщо 
і 
відрізняються лишень на дкілька одиниць останнього зберігаючого десяткового розряду, то можна поставити 
а потім знайшовши 
перерахувавши кінцеві різниці (7). Після цього, потрібно знову знайти по формулі (8) Поту цей крок h повинен бути таким, щоб цей перерахунок був зміненим.
На практиці крок h вибирають малим, щоб можна було знехтувати членом 
в формулі (8)
Якщо за розбіжність величин 
і 
суттєва, то потрібно зменшити крок h .
Звичайно крок h зменшують рівно в 2 рази. Можна показати, як в цьому випадку, маючи до деякого значення і таблицю величин х j , yj , Yj = hy ’ j ( j <= i ) з кроком 
, можна просто побудувати таблицю величин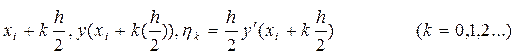 
з кроком 
На основі формули (4) будемо мати
(9)
Де 
Звідси, 
і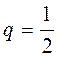 
і враховуючи, що 
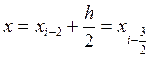заходимо
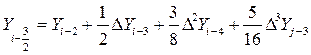(10)
Аналогічно при 
із формули (9) отримаєм, що аргументу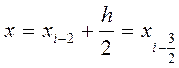 
відповідає значення
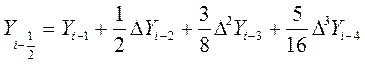(11)
Що стосується значень Yi -1 i Yi , то вони знаходяться в старій таблиці. Після цього складаємо початковий відрізок для нової таблиці:
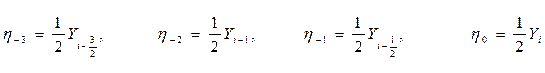
і знаходимо кінцеві різниці:
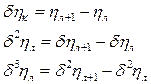
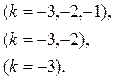
Далі таблиця будується простим способом, подальшою модифікацією формули (5):
Для роботи на компютерах формулу Адамса (5) вигідно використовувати в розкритому виді. Враховуючи, що
Після цього маємо: 
причому 
Метод Крилова
Для спрощеня запису обмежимось розглядом диференціальних рівнянь першого порядка
(1)
З початковими умовами 
Введемо спочатку ряд допоміжних формул
