Курсовая работа: Деякі скінченно-різнецеві методи розвязування звичайних диференціальних рівнянь

x_{n +1} ≡ x(t_n +∆t ) в ряд Тейлора. Запишемо

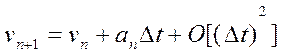(3)

і

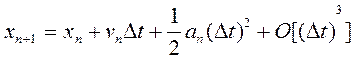(4)

Добре відомий метод Ейлера еквівалентний збереженню в формулі (3) членів

(5)

і

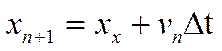(6)

Оскільки ми утримали у формулах (5-6) члени порядку ∆t, то «локальна» погрішність (погрішність на кроці) складає величину O(∆t)²

Оскільки ми від кроку до кроку погрішності накопичуються, позтому можна припускати, що «глобальна» погрішність, що є сумарною погрішністю за розглядом проміжок часу, буде величиной O(∆t). Ось ця оцінка погрішності цілком правдоподібна, оскільки число кроків, на яке розбивається часовий інтервал, пропорційна 1/∆t . Звідси випливає, порядок глобальної погрішності збільшується в ∆t разів по відношенню до локальної погрішності. Оскільки прийнято "говорити, що метод має n-й порядок аппроксимації, якщо ця локальна погрішність рівна О((∆t)^{n +1} ), то метод Ейлера відноситься до методів першого порядку.

Метод Ейлера являється асиметричним, оскільки він просуває вирішення на один часовий крок ∆t, а використовує при цьому інформацію про похідну тільки в початковій точці інтервалу. Ми вже переконалися в тому, що точність методу Ейлера обмежується і частенько породжуване його рішення нестійке. На щастя, як правило, немає необхідності використовувати більш складні алгоритми. Наприклад, швидше ми знайшли, що проста модифікація методу (5-6), запропонована Кромером і іншими авторами, породжує стійке рішення для коливальних систем. Для закріплення повторимо алгоритм Ейлера-Кромера або наближення по «останній точці»:

(7)

і

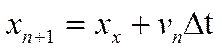(8)

Мабуть найбільш очевидний шлях удосконалення методу Ейлера, полягає в використанні для обрахування нового значення координати середини на відрізку швидкості. Відповідний метод середньої точки можна записати в вигляді:

(9)

і

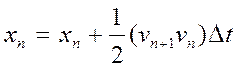(10)

Замітимо, що якщо підставити вираз (9) для v_{n +1} в (10) то отримаємо

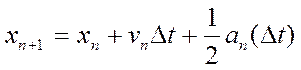(11)

Звідси випливає, що метод середньої точки другого порядку точності по координаті і першого порядку по швидкості. Хоча наближення по середній точці дає точні результати для випадку постійного прискорення, взагалом він не приводить до значного покращення результату, ніж метод Ейлера. На справді оці два методи однаково погані, оскільки з кожним кроком погрішність збільшується.

Метод напівкроку відноситься до методів більше за високого порядок точностіз обмеженою погрішністю. Приймається, що средияя скорість на відрізку рівна значенню швидкості в середиие відрізок. Метод напівкроку можна записати у виді:

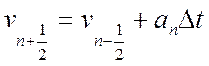(12)

і

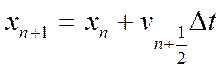(13)

Замітио, що метод напів кроку не являє собою «самостартючим», так чи однакще фомули не дозволять порахвати v_1/2. Цю незручність модна здолати поклавши

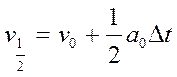(14)

Оскільки формули (12-14) можна повторювати до безмежності, то метод напів кроку отримав широке розповсюдження в навчальній літературі.

Один із найбільш відомих алгоритмів вищого порядку привласнюєтья Верле. Запишемо в ряд Тейлора для х_{n -1}