Курсовая работа: Деякі скінченно-різнецеві методи розвязування звичайних диференціальних рівнянь
Виконав:
студент групи ПМ-41
Васьків Святослав
Перевірив:
науковий керівник:
Василишин П.Б.
Івано-Франківськ 2010
План
Вступ.
1. Чисельна ітерація рівнянь Ньютона
2. Алгоритм Бімана і Шофілда
3. Метод Рунге-Кутта
a) Метод Рунге — Кутта 4-го порядку
б) Неявні схеми Рунге-Кутта
в) Неявні інтерполяційні схеми
г) Програма Рунге-Кутта на мові С#
д) Програма Beeman
4. Метод Адамса
5.Метод Крилова
6. Метод Чаплигіна
Висновок
Список використаної літератури
Вступ
Приведемо декілька найбільш відомих скінченно-різнецевих методів рішення рівнянь руху з непереривною силою. Важливо пам'ятати про те, що успішне використання чисельного метода визначається не лише тим, наскільки добре він наближає похідну на кожному кроці, але і тим, наскільки добре він апроксимує інтеграли руху, наприклад повну енергію. Безліч алгоритмів, використовуються в наш час, свідчить про те, що жоден метод не перевершує по усіх параметрах усіх інших.
1. Чисельна ітерація рівнянь Ньютона
Для спрощення запису розглянемо одновимірний рух частини і запишемо рівняння Ньютона у виді:
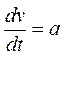 (1)
(1)
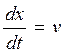 (2)
(2)
Метою усіх скінцеворізнецевих методів являється знаходження значень x n +1 і v n+1 (точка в "фазовому просторі") у момент часу tn+1 =tn +∆t Нам вже відомо, що величину кроку ∆t потрібно вибирати таким чином, щоб метод інтегрування породжував приймати однакове рішення. Один із способів перевірки стійкості методу полягає в контролі величини повною енергії і забезпеченні того, щоби вона не відхилялася від початкового значення у разі, коли повна енергія зберігалась. Досить велике значення кроку приводить до не збереження повної енергії і до різних розв’язків для хn +1 i vn+1 , тобто до таких розв’язків, які все більше відхиляються з потоком часу від істинного розв’язку.
Суть багатьох алгоритмів, можна зрозуміти, розкладаючи
--> ЧИТАТЬ ПОЛНОСТЬЮ <--