Курсовая работа: Деякі скінченно-різнецеві методи розвязування звичайних диференціальних рівнянь

(15)

Якщо скласти формули інтегрування вперед і назад (вирази (3) і (14) відповідно) то отримаємо

(16)

або

(17 )

Аналогічно розв'язання розкладу в ряд Тейлора для x_{n +1} i x_{n -1} дає

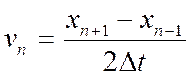(18)

Підмітимо, що звязок з алгоритом Верле (18) велика погрішність має третій порядок для координати і другий порядок для швидкості. Проте швидкість не бере участі в інтегруванні рівнянь руху. В літературі по чисельному аналізу алгоритм Верле називається «неявна симетричність різновидної схеми».

Менш відомим, про те математично еквівалентної версії алгоритму Верле являє собою схема

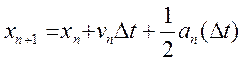(19)

і

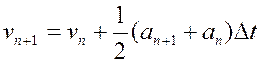(20)

Видно, що схема (19-20), називається швидкісною формулою алгоритму Верле, являється самостартуючою і не приводить до накопичення погрішностей округлення. Формули (19-20) можна вивести із формул (16-19) наступним чином.. Спочатку додамо і віднімемо із рівнянь (16-19) по (1/2)х_{n +1} і запишемо:

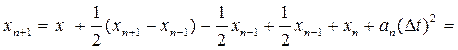
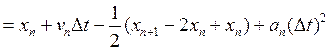(21)

Тут ви використаємо вираз (18). Із (17) знайдемо а_n для метода Верле:

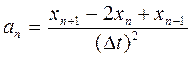(22)

Легко помітити, що підстановка (22)в вираз (21) приводить до (19). В томуж дусі перепишемо (17) для v_{n +1}

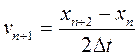(23)

Тепер перепишемо формулу (17) для х_{n +2} і підтавимо її в отриманий результат формули (23). Отримуємо:

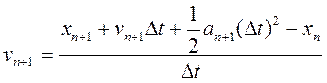(24)

Тоді використовуємо вираз (17) для x_{n +1,} повторимо цю процедуру і поставимо x_{n +1} в (24); після не важких перестановок отримаємо потрібний результат (20)

2. Алгоритм Бімана і Шофілда

Інший корисний алгоритм, в якому немає нагромаження погрішностей округлення, як в алгоритмі Верле, належить Біміану і Шофілду. Запишемо алгоритм Бімана в наступному виді:

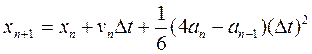(25а)

і

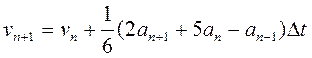(25б)

Підмітимо, що точність розразунку траєктторії по схемі (25) не вища, ніж в алгоритмі Верле. Її перевага заключається в тому, що просто вона краще зберігає енергію. Однак алгоритм Бімана не самостартуючий. Алгорим Бімана і алгоритм Верле в швидкісній вормулі викоритані в програмі BEEMAN

Завершимо наше обговорення оротким викладом двох методів, які зазвичай приводяться в підручниках по чисельному аналізу. Один приклад метода предиктор: