Курсовая работа: Деякі скінченно-різнецеві методи розвязування звичайних диференціальних рівнянь

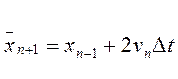(26а)

Передбучуване значення коодринати дозволить оприділити прискорення

Тоді, використовуючи , отримаємо скоректироване з начення v_{n +1} і x_{n +1}

коректор: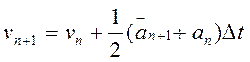

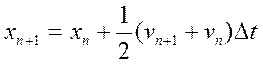(26б)

Скоректироване значення x_{n +1} використовується для визначення нового передбачуваного значення а_{n +1} і, значить, нових передбачених значень v_{n +1} i x_{n + r} Ця процедура повторяється до тих пір, доки передбачення і скоррективонане значення x_{n +1} відрізняються менше ніж на задану величину! Даний метод можна розробити на схемі більш високого порядку, які зв’язуються між собою не тільки x_{n +1 ,} x_n і v_n , але і так само значеннями v_{n -1} і v_{n -2.} Замітимо, що метод предиктора-коректора не являється самостартуючим.

3. Метод Рунге-Кутта

Для пояснення методу Рунге-Кутта подивимось спочатку розв’язок диференціального рівняння першого порядку

(27)

Метод Рунге-Кутти другого порядку для розв’язку рівняння (27) модна, використовуючи стандартні значення, записати наступним чином:

(28)

Сенс формул (28) полягає у наступному: В методі Ейлера допускається, що для екстаполяції в наступну точку модна використовувати нахил кривої f(x_n ,y_n )в точці (x_n ,y_n ) так чи однакше y_{n +1} =y_n +f(x_n ,y_n )*∆x. Однак можна повисити почність оцінки нахилу, якщо методом Ейлера повести екстраполяцію в середню точку відрізку, а потім використати центральну похідну на всьому відрізку. Звідси оцінка нахилу в методі Рунге-Котти рівна

де

Застосування методу Рунге-Кутти до рівнянь руху Ньютона дає

(29)

Оскільки методи Руиге-Кутти є такими, що самостартуючими, то їх часто використовують для вираховання декількох перших кроків для несамостартуючих алгоритмів.

4. Метод Рунге — Кутта 4-го порядку

Цей метод настільки широко розповсюджений, що його часто називають просто методом Рунге — Кутта.

Розглянемо задачу Коші для системи диференціальних рівнянь довільного порядку, що записується у векторній формі як:

Тоді значення невідомої функції в точці x_{n +1} обчислюється відносно значення в попередній точці x_n по такій формулі:

де h— крок інтегрування, а коефіцієнти k _n розраховуються наступним чином:

Це метод 4-го порядку, тобто похибка на кожному кроці становить O ( h ⁵ ) , а сумарна похибка на кінцевому інтервалі інтегрування є величиною O ( h ⁴ ) .

Прямі методи Рунге — Кутта

Група прямих методів Рунге — Кутта є узагальненням методу Рунге — Кутти 4-го порядку. Воно задається формулами

де