Курсовая работа: Дифференциальные системы эквивалентные автономным системам с известным первым интегралом

Наряду с исходной дифференциальной системой

будем рассматривать множество возмущённых систем

где непрерывная скалярная нечётная функция, а произвольная непрерывно дифференцируемая вектор-функция. Выясним вопрос об эквивалентности в смысле совпадения отражающих функций дифференциальных систем (1) и (2). При совпадении отражающих функций двух систем совпадают их операторы сдвига на симметричном промежутке вида и, значит, для периодических систем совпадают их отображения за период .

Как известно, отражающая функция системы (1) обязана удовлетворять соотношению

Если вектор-функция, а

вектор-столбец, то полагаем

,

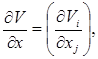
Лемма 1.

Для любых трёх вектор-функций из которых функция дважды непрерывно дифференцируема, а функции и дифференцируемы, имеет место тождество

Лемма 2 .

Пусть отражающая функция системы с непрерывно дифференцируемой правой частью. Тогда для каждой непрерывно дифференцируемой вектор функции функция

удовлетворяет тождеству

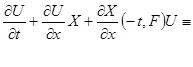
Доказательство. Учитывая соотношение , простыми выкладками установим тождества

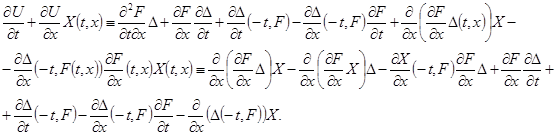
К первым двум слагаемым последней части этого тождества применим тождество . Тогда после несложных формальных преобразований придём к соотношению

Прибавим к левой и правой частям этого соотношения выражение придём к нужному нам тождеству

Лемма доказана.

Теорема 1

Пусть вектор-функция является решением дифференциального уравнения в частных производных