Курсовая работа: Динамика работы и расчет времени срабатывания электромагнита постоянного тока с пользованием математического пакета MathCad в среде Windows

2.3.1 Определение изменения тока и напряжения во времени численным методом

Численный метод состоит в составлении системы дифференциальных уравнений, описывающей работу электромагнита. Далее эта система решается с помощью MACHCAD, с использованием матрицы системы. Матрица системы составляется из коэффициентов дифференциальных уравнений. Отдельно составляется матрица начальных условий.

Уравнение

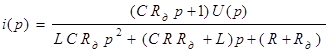
можно записать и в виде уравнений в нормальной форме Коши:

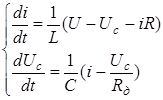
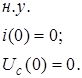
СПРАВКА: В Mathcad 11 имеются три встроенные функции, которые позволяют решать задачу Коши различными численными методами.

· rkfixed(y0, t0, t1, N, D) — метод Рунге-Кутты с фиксированным шагом,

· Rkadapt(y0, t0, t1, N, D) — метод Рунге-Кутты с переменным шагом;

· Buistoer(y0, t0, t1, N, D) — метод Булирша-Штера;

o у0 — вектор начальных значений в точке to размера NXI;

o t0 — начальная точка расчета, t1 — конечная точка расчета,

o N — число шагов, на которых метод находит решение;

o D — векторная функция размера NXI двух аргументов — скалярного t и векторного у. При этом у — искомая векторная функция аргумента t того же размера NXI.

Воспользуемся функцией Rkadapt(y0, t0, t1, N, D) -получим матрицу решения системы обыкновенных дифференциальных уравнений численным методом Рунге-Кута на интервале от t0 до t1 (зададим от 0 до 5 сек) при N фиксированных шагах решения (пусть N=1000), вектор заданных начальных условий X0 (нулевые условия). Сформируем матрицу системы дифференциальных уравнений 2-го порядка.

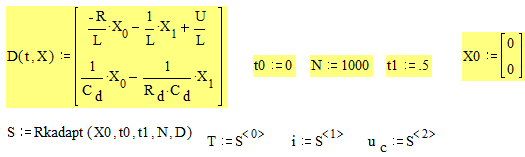Применим функцию: Rkadapt

-Интервал времени- нулевой столбец матрицы решений S.

-Значение искомой величины тока- первый столбец матрицы решений S.

напряжение на конденсаторе - второй столбец матрицы S

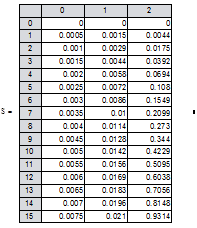
И так далее 1000 значений (N=1000)

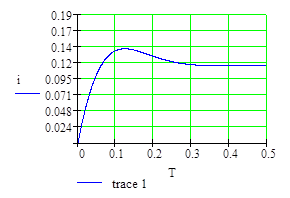
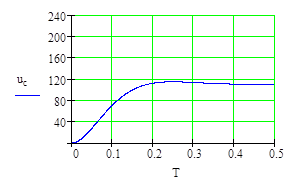
Рис. 2.4. Графики зависимости тока в катушке электромагнита и напряжения на конденсаторе от времени при ускоренном срабатывании электромагнита (численное решение)

2.3.2 Решение дифференциальных уравнений с помощью преобразований Лапласа