Курсовая работа: Дисперсионный анализ показателей смертностей населения Нерюнгринского улуса

, (8)

где α – уровень значимости; n – количество факторов; k – количество испытаний.

Если F _набл <F _кр , то гипотеза о равенстве дисперсий будет принята.

Если число испытаний на разных уровнях различно (q ₁ испытаний на уровне F ₁ , q ₂ – на уровне F ₂ , …, q_р - на уровнеF _р ), то [1]:

, (9)

где сумма квадратов наблюдавшихся значений признака на уровне F_j ,

сумма наблюдавшихся значений признака на уровне F_j .

При этом объем выборки, или общее число испытаний, равен . Факторная сумма квадратов отклонений вычисляется по формуле [1]:

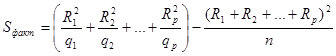. (10)

Остальные вычисления проводятся так же, как в случае одинакового числа испытаний [1]:

. (11)

1.2. Линейный множественный регрессионный анализ

Регрессионный анализ, по-видимому, наиболее широко используемый метод многомерного статистического анализа. Термин ''множественная регрессия'' объясняется тем, что анализу подвергается зависимость одного признака (результирующего) от набора независимых (факторных) признаков. Разделение признаков на результирующий и факторные осуществляется исследователем на основе содержательных представлений об изучаемом явлении (процессе). Все признаки должны быть количественными (хотя допускается и использование дихотомических признаков, принимающих лишь два значения, например 0 и 1).При поведении экспериментов в множественной ситуации исследователь записывает показания приборов о состоянии функции отклика (y) и всех факторов, от которых она зависит (x_i ).

При построении регрессионных моделей, прежде всего, возникает вопрос о виде функциональной зависимости, характеризующей взаимосвязи между результирующим признаком и несколькими признаками-факторами. Выбор формы связи должен основываться на качественном, теоретическом и логическом анализе сущности изучаемых явлений. Чаще всего ограничиваются линейной регрессией, т.е. зависимостью вида [2]:

Y=a₀ +a₁ x₁ +a₂ x₂ +…+a_n x_n (12)

где Y - результирующий признак; x₁ , …, x_n - факторные признаки; a₁ ,…,a_n - коэффициенты регрессии; а₀ - свободный член уравнения. a_i находим методом наименьших квадратов, для этого рассматривается функции [2]:

(13)

Находим частные производные по неизвестным переменным, приравниваем к нулю и получаем систему уравнений. Решая систему, можем найти наименьшее значение функции.

Так как запись множественной регрессии (линейной) в матричной форме имеет вид [2]:

Y=X*A, (14)

где Y - это вектор-столбец опытных значений изучаемой характеристики; X –матрица всех значений всех рассматриваемых факторов, полученных при проведении измерений или наблюдений; А – вектор-столбец искомых коэффициентов аппроксимирующего полинома (12) [2]:

Y= ; (15)

X=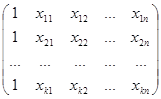; (16)

Y=; (17)

Тогда функционал F метода наименьших квадратов имеет вид [2]:

(18)

Для оценки адекватности рассчитанной регрессионной модели вычисляется коэффициент детерминации, он показывает, какая часть дисперсии функции отклика объясняется вариацией линейной комбинации выбранных факторов x₁ , x₂ ,…, x_j , x_n [2]:

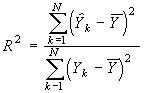, (19)

где - прогнозные значения