Бухгалтерский учет и аудит / Курсовая работа: Дисперсионный анализ показателей смертностей населения Нерюнгринского улуса

Курсовая работа: Дисперсионный анализ показателей смертностей населения Нерюнгринского улуса

F набл =14, 1090;

F кр (0,01; 15; 18)= 3,23.

Сравнивая полученные значения, мы делаем вывод о том, что различия между дисперсиями не значимо, то есть фактор (заболевания) оказывает существенное влияние на функцию отклика (смертность). Следовательно, среднее наблюдаемое значение на каждом уровне (групповые средние) различаются значимо.

2.3. Построение уравнения множественной регрессии

Следующим этапом, мы построим уравнение множественной регрессии. Для этого мы воспользовались Пакетом анализа данных для вычисления основных статистических параметров выборки. Для того чтобы отыскать команду вызова надстройки Пакет анализа в MicrosoftExcel, необходимо воспользоваться меню Сервис – Анализ данных.… В появившемся диалоговом окне выбрать пункт Регрессия. В поле Входной интервал Y: указать диапазон значений нашего у, в поле Входной интервал X: указать все значения наших x. В разделе параметры вывода указать Выходной интервал: ввести любую, удобную для вас ячейку. Результаты работы режима Регрессия представлен в таблице 3 [см. Приложение]. Таким образом, наше уравнение регрессии имеет вид:

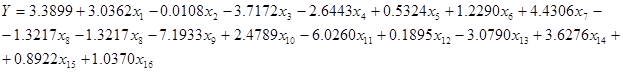
2.4. Исключение незначимых факторов

Для того чтобы исключить заболевания, которые оказывают незначительное влияние на смертность население, вначале рассчитаем парные коэффициенты корреляции по формулам (21), (22), и построим корреляционную матрицу (см. таблицу 4 [Приложение]). Используя полученную матрицу, вычислим по формуле (28) частные коэффициенты корреляции, получим:

Ryx1 0,012345 Ryx9 -0,85883735
Ryx2 0,79942633 Ryx10 -0,9606058
Ryx3 0,01902545 Ryx11 -0,66239756
Ryx4 -0,7279617 Ryx12 -0,81452592
Ryx5 0,25701348 Ryx13 -0,16934424
Ryx6 0,30479306 Ryx14 0,9030776
Ryx7 -0,9799582 Ryx15 0,10681524
Ryx8 0,96909722 Ryx16 0,97533032

Сравнивая частные коэффициенты корреляции и парные коэффициенты, исключаем незначительные факторы. Факторы, которые после сравнения этих коэффициентов оказались незначимы, можно исключить из уравнения регрессии. В уравнение регрессии, которое мы получили, таковыми оказались x1 , x3 , x4 , x9 , x10 , x11 , x12 , x13 и x16 . То есть инфекционные и паразитарные заболевания, болезни эндокринной системы, расстройства питания и нарушения обмена веществ, психические расстройства и расстройства поведения, болезни костно–мышечной системы и соединительной ткани, болезни мочеполовой системы, беременность, роды и послеродовый период, врожденные аномалии (пороки развития), отравления и некоторые другие последствия воздействия внешних причин, отдельные состояния, возникающие в перинатальном периоде не оказывают существенного влияния на смертность.

Так как мы исключили некоторые факторы, уравнение регрессии изменилось, поэтому необходимо вновь, воспользовавшись Пакетом Анализ данных, построить новое уравнение регрессии (см. таблицу 5 [Приложение]). Теперь уравнение представимо в виде:

Данное уравнение отображает функциональную связь между смертностью и различными классами заболеваний.


Заключение

В данной курсовой работе рассмотрены заболевания, влияющие на изменение смертности Нерюнгринского улуса. Были выбраны факторы, методом исключения эффектов, приводящие к высокой смертности. Применяя методы теории вероятностей и математической статистики, было построено уравнение, показывающее зависимость изучаемого явления (смертности) от выбранных факторов (классов заболеваний).

Проведя анализ полученной модели, выяснилось, что наиболее часто приводят к летальному исходу болезни системы кровообращения, таким образом, этот класс заболеваний стоит на первом месте. На втором месте стоят внешние причины заболеваемости и смертности, и на третьем – новообразования.

В заключении, необходимо отметить, что профилактика именно этих заболеваний приведет к уменьшению показателя летальности и позволит преодолеть демографический кризис.


Список литературы

1. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов. - М.: Высш. шк., 1997.

2. Львовский В.Н. Статистические методы построения эмпирических формул: Учеб. пособие для вузов. - М.: Высш. шк., 1988.

3. Вентцель Е.С. Теория вероятностей: Учебник для вузов. - М.: Высш. шк., 1999.

4. «Многомерный статистический анализ на ЭВМ с использованием пакета MicrosoftExcel»/М., 1997.

5. «Государственный доклад о состоянии здоровья населения Нерюнгринского улуса в 2006 году»; (редкол.:Вербицкая Л.И. и др.), 2007.


Приложение

Таблица 1

Исходные данные

XVI 1 1 2 4 11 11 11 16 13 11 15 11 2 5 1 1 0 0
XV 0 0 0 0 0 0 0 1 0 2 0 2 1 0 0 0 0 0
XIV 1 0 0 0 1 1 1 1 0 1 5 4 2 4 2 1 3 2
XIII 2 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
XII 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
XI 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
X 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0
IX 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
VIII 0 0 0 0 0 0 1 3 3 4 9 5 3 6 2 0 0 0
VII 1 0 0 0 0 2 2 1 3 5 6 2 2 1 1 0 1 0
VI 0 1 0 0 0 4 1 8 17 32 47 41 29 59 35 24 21 8
V 0 0 1 0 0 0 0 2 1 0 1 2 1 1 0 0 0 0
IV 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0
III 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0
II 0 0 0 0 1 3 0 2 8 14 17 20 11 15 12 3 4 1
I 0 0 0 0 0 1 0 2 0 3 0 1 0 1 0 0 0 0
Количество смертей 7 3 3 8 15 29 20 38 50 79 110 88 54 98 56 34 45 20
Возраст до года 1-5 11-17 17-19 20-24 25-29 30-34 35-39 40-44 45-49 50-54 55-59 60-64 65-69 70-74 75-79 80-84 85 и более

Таблица 2

Факторный анализ

Возраст I II III IV V VI VII VIII IX X
R1 P1 R2 P2 R3 P3 R4 P4 R5 P5 R6 P6 R7 P7 R8 P8 R9 P9 R10 P10
до года 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0
1-5 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0
11-17 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0
17-19 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
20-24 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
25-29 1 1 3 9 0 0 0 0 0 0 4 16 2 4 0 0 0 0 0 0
30-34 0 0 0 0 0 0 0 0 0 0 1 1 2 4 1 1 1 1 0 0
35-39 2 4 2 4 1 1 0 0 2 4 8 64 1 1 3 9 0 0 0 0
40-44 0 0 8 64 0 0 0 0 1 1 17 289 3 9 3 9 0 0 1 1
45-49 3 9 14 196 1 1 1 1 0 0 32 1024 5 25 4 16 0 0 0 0
50-54 0 0 17 289 0 0 0 0 1 1 47 2209 6 36 9 81 0 0 0 0
55-59 1 1 20 400 0 0 0 0 2 4 41 1681 2 4 5 25 0 0 0 0
60-64 0 0 11 121 0 0 0 0 1 1 29 841 2 4 3 9 0 0 0 0
65-69 1 1 15 225 0 0 0 0 1 1 59 3481 1 1 6 36 0 0 1 1
70-74 0 0 12 144 0 0 0 0 0 0 35 1225 1 1 2 4 0 0 0 0
75-79 0 0 3 9 1 1 0 0 0 0 24 576 0 0 0 0 0 0 0 0
80-84 0 0 4 16 0 0 0 0 0 0 21 441 1 1 0 0 0 0 0 0
85 и более 0 0 1 1 0 0 0 0 0 0 8 64 0 0 0 0 0 0 0 0
∑ 8 16 111 1479 3 3 1 1 9 13 327 11913 27 91 36 190 1 1 2 2
R1 ² 64 12321 9 1 81 106929 729 1296 1 4

Продолжение таблицы 2

XI XII XIII XIV XV XVI
R11 P11 R12 P12 R13 P13 R14 P14 R15 P15 R16 P16
0 0 4 16 2 4 1 1 0 0 1 1
0 0 0 0 1 1 0 0 0 0 1 1
0 0 0 0 1 1 0 0 0 0 2 4
0 0 0 0 0 0 0 0 0 0 4 16
0 0 0 0 1 1 1 1 0 0 11 121
1 1 0 0 0 0 1 1 0 0 11 121
0 0 0 0 0 0 1 1 0 0 11 121
0 0 0 0 0 0 1 1 1 1 16 256
0 0 0 0 0 0 0 0 0 0 13 169
0 0 0 0 0 0 1 1 2 4 11 121
0 0 0 0 0 0 5 25 0 0 15 225
0 0 0 0 0 0 4 16 2 4 11 121
0 0 0 0 0 0 2 4 1 1 2 4
0 0 0 0 0 0 4 16 0 0 5 25
0 0 0 0 0 0 2 4 0 0 1 1
0 0 0 0 0 0 1 1 0 0 1 1
0 0 1 1 0 0 3 9 0 0 0 0
0 0 0 0 0 0 2 4 0 0 0 0
1 1 5 17 5 7 29 85 6 10 116 1308
1 25 25 841 36 13456

I. некоторые инфекционные и паразитарные заболевания.

II. новообразования.

III. болезни эндокринной системы, расстройства питания и нарушения обмена веществ.

IV. психические расстройства и расстройства поведения.

V. болезни нервной системы.

VI. болезни системы кровообращения.

VII. болезни органов дыхания.

VIII.болезни органов пищеварения.

IX. болезни костно–мышечной системы и соединительной ткани.

X. болезни мочеполовой системы.

XI. беременность, роды и послеродовый период.

XII. отдельные состояния, возникающие в перинатальном периоде.

XIII.врожденные аномалии (пороки развития), деформации и хромосомные нарушения.

XIV.симптомы, признаки и отклонения от нормы, не классифицированные в других рубриках.

XV. травмы, отравления и некоторые другие последствия воздействия внешних причин.

XVI.внешние причины заболеваемости и смертности.


Таблица 3

Уравнение регрессии

Регрессионная статистика
Множественный R 1,0000
R-квадрат 0,9999
Нормированный R-квадрат 0,9986
Стандартная ошибка 1,2381
Наблюдения 18,0000
Дисперсионный анализ
df SS MS F Значимость F
Регрессия 16,0000 19025,4116 1189,0882 775,7397 0,0282
Остаток 1,0000 1,5328 1,5328
Итого 17,0000 19026,9444
Коэффициенты Стандартная ошибка t-статистика P-Значение Нижние 95% Верхние 95% Нижние 95,0% Верхние 95,0%
Y-пересечение 3,3899 1,2355 2,7438 0,2225 -12,3082 19,0880 -12,3082 19,0880
Переменная X 1 3,0362 2,2817 1,3307 0,4103 -25,9556 32,0281 -25,9556 32,0281
Переменная X 2 -0,0108 0,5682 -0,0190 0,9879 -7,2301 7,2085 -7,2301 7,2085
Переменная X 3 -3,7172 3,5010 -1,0618 0,4809 -48,2011 40,7668 -48,2011 40,7668
Переменная X 4 -2,6443 9,9430 -0,2659 0,8345 -128,9822 123,6936 -128,982 123,693
Перем?

К-во Просмотров: 286
Бесплатно скачать Курсовая работа: Дисперсионный анализ показателей смертностей населения Нерюнгринского улуса