Курсовая работа: Дисперсионный анализ показателей смертностей населения Нерюнгринского улуса

. (20)

Значение коэффициента множественной корреляции оценивается с помощью таблицы 2 [1]:

Таблица Чеддока Таблица 2

диапазон измерения	характер тесноты
	слабая
	умеренная
	заметная
	высокая
	весьма высокая

1.3. Множественный корреляционный анализ

Расчеты обычно начинают с вычисления парных коэффициентов корреляции, характеризующих тесноту связи между двумя величинами. В множественной ситуации вычисляют два типа парных коэффициентов корреляции:

1. - коэффициенты, определяющие тесноту связи между функцией отклика y и одним из факторов [2]:

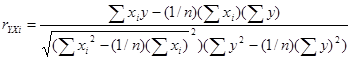. (21)

2. - коэффициенты, показывающие тесноту связи между одним из факторов x_i и фактором x_m (i, m=) [2]:

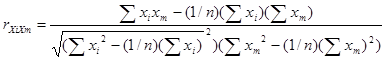(22)

.

Значение парного коэффициента изменяется, как указывалось выше, изменяется от -1 до +1. Если, например, коэффициент - величина отрицательная, то это значит, что x_i уменьшается с увеличением y. Если положителен, то x_i увеличивается с увеличением y.

Значимость парных коэффициентов корреляции можно проверить двумя способами:

1)сравнение с табличным значениями [2]:

, (23)

2) по t-критерию Стьюдента [2]:

, (24)

Где - среднеквадратическая погрешность выборочного парного коэффициента корреляции [2]:

. (25)

Здесь определяется по таблице с числом степеней свободы .

Доверительный интервал для парных коэффициентов корреляции [2]:

, (26)

где - парный коэффициент корреляции в генеральной совокупности.

Если один из коэффициентов окажется равным 1, то это означает, что факторы x_i и x_m функционально (не вероятностно) связаны между собой и тогда целесообразно один из них исключить из рассмотрения, причем оставляют тот фактор, у которого коэффициент больше.

После вычисления всех парных коэффициентов корреляции и исключения из рассмотрения того или иного фактора можно построить матрицу коэффициентов корреляции вида [2]:

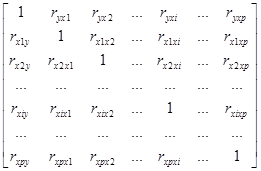. (27)

Используя матрицу (23) можно вычислить частные коэффициенты, которые показывают степень влияния одного из факторов x_i на функцию отклика y при условии, что все остальные факторы закреплены на постоянном уровне. Формула для вычисления частных коэффициентов корреляции такова [2]:

, (28)

где - определитель матрицы, образованной из матрицы (27) вычеркиванием 1-й строки, i-го столбца. Определители , вычисляются аналогично. Как и парные коэффициенты, частные коэффициенты корреляции изменяются от -1 до +1.

2. Аналитическая часть