Курсовая работа: Дослідження чисельних методів вирішення нелінійних рівнянь
Отже, потрібно брати такі приблизні значення початкових наближень: -1,8; 0,1; 1,8. Дійсно ці значення задовольняють необхідну умову 
. При значенні х0 =0,1 (f’(x0 ))2 =99,9, a добуток f’’(x0 )f(x0 )=5*10-10 , що є меншим за значення першої похідної, піднесеної до квадрату. При значеннях х0 = -1,8 ; х0 =1,8 також виконуються дані співвідношення.
Для знаходження комплексних коренів нелінійного рівняння окрім звичайних методів, які аналогічні тим, що використовуються для знаходження дійсних коренів, існує низка спеціальних методів, що дозволяють оцінювати комплексні корені проводячи обчислення з дійсними числами. Більшість цих методів базується на перетворені початкового нелінійного рівняння до добутку квадратичних співмножників.
Щоб знайти комплексні корені нелінійного рівняння розкладемо задане рівняння 
на найпростіші множники. В результаті отримаємо такий многочлен:
, де 1,75; 1,8; 0,1 – дійсні корені рівняння. Прирівнявши перший множник до нуля , знайдемо приблизні значення комплексних коренів рівняння, яких має бути два:
;дискримінантD=0.0025-12.61= -12.6<0
; 
3. Алгоритм методів
На основі теоретичного матеріалу, розглянутого в попередньому розділі роботи, було розроблено алгоритми методів.
Алгоритм розвязку нелінійного рівняння методом Ньютона за допомогою ЕОМ є досить простим і полягає в тому, що спочатку задається дане вихідне рівняння, його похідна, а також допустима похибка. Потім використовуючи вищеописану ітераційну формулу знаходять ряд значень х:
хn +1 = хn -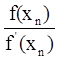
,
де хn +1 – значення х на наступній ітерації, а хn – значення х на попередній ітерації. Ця операція повторюється до тих пір, поки не виконається умова 
<Δ, тобто різниця значень наступної ітерації і попередньої менше за задану похибку.
Алгоритм розвязку цього ж рівняння за методом хорд полягає в тому, щовизначаються значення функції до зміни знаку при переході від 
до 
поки кінці інтервалів xn +1 , хn не будуть мати різні знаки.
Після цього визначають f(x*) і порівнюють його з f(xn ). Надалі користуються xn +1 замість того значення, з яким воно збіглося за знаком.
Знаходимо ряд значень х до тих пір, поки не виконається умова
< Δ де Δ - задана допустима похибка.
Блок-схеми даних методів наведені в додатку А.
3.1 Вибір інструментальних засобів
Для вирішення цієї задачі було обрано середовище програмування С, так як воно має ряд вагомих переваг перед іншими середовищами і мовами програмування. Зокрема такими перевагами є те, що:
- не вимагає великих затрат як апаратної частини комп’ютера так і програмної
- дозволяє досить просто реалізовувати поставлені задачі
- є дуже візуальним і наглядним що робить його зручним інструментом в користуванні
- ця мова є досить гнучка і дозволяє використовувати технології обєктно-орієнтованого програмування.
3.2 Вхідні та вихідні дані
Для даних методів розв’язку нелінійного рівняння вхідними даними є початкове рівняння; похідна від нього; початкові наближення х0 (1,75; -1,8; 0,1) і допустима похибка Δ, яка вводиться з клавіатури .
Вихідними даними є знайдені корені х, які задовольняють умову:
< Δ та кількість кроків для отримання розвязку із заданою похибкою.
3.3 Структура програми
Програму можна умовно розділити на чотири такі частини:
1. блок опису вхідних та вихідних даних
2. введення початкових даних
3. процедури розвязку рівняння методом хорд та Ньютона