Курсовая работа: Доведення теоретико-математичних тотожностей і тверджень

7.2. Алгоритм рішення задачі

7.3. Блок-схема програми

7.4. Вихідний текст програми

7.5. Результат роботи програми

Список літератури

1. Доведення рівностей методом математичної індукції

Теоретичні відомості

ТЕОРЕМА. Нехай властивість Р вірна для п =1 і нехай з істинності Р для п = к випливає його істинність для п = к+1 . Тоді властивість Р вірна для кожного .

ТЕОРЕМ А. Нехай множина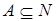має такі властивості.

1. .

2. Для кожного , якщо , то .

Тоді .

ТЕОРЕМА(Зворотний метод математичної індукції) . Нехай властивістьр (n ) виконується дляn=1. з того, що вона вірна для кожного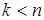випливає, щор (n ) вірна дляn . Значитьр (n ) вірна для будь-якого натуральногоn .

Зауваження. У загальному випадку індуктивний процес не зобов'язаний починатися з 1. Базисом індукції може бути будь-як ціле число a .

ТЕОРЕМА. Нехай властивістьр (n ) виконується дляn= a . З цього для кожного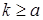випливає істинність дляk +1. Значитьр (n ) істинно для будь-якого цілого.

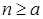Завдання 1: Довести, що для будь-якого

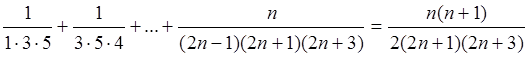(1)

Розв‘язок:

1. Базиси індукції . Перевіримо рівність для п =1. Ліва частина =, права частина = . Тобто базис індукції виконується.

2. Індуктивне припущення . Вважаємо рівність (1) вірною для п = к , тобто припустимо, що:

(2)

3. Індуктивний перехід . Доведемо рівність (1) для п=к+1 , тобто доведемо, що: ,звідси =

Таким чином на підставі методу математичної індукції рівність (1) вірна для кожного п .

2 . Розробка алгоритму та написання програми обчислення множин

2.1. Теоретичні відомості

Множина – це будь-яка певна сукупність об'єктів. Об‘єкти з яких складається множина, називаються його елементами .

Множина, що не містить елементів, називається порожньою.

Множини, як об’єкти, можуть бути елементами інших множин. Множини, елементи яких є множини, іноді називають сімейством .

Сукупність об'єктів, які не є множиною, називають класом .

Звичайно в конкретних міркуваннях елементи всіх множин беруться з деякого одного, достатньо широкої множини U яке називається універсальною множиною.

Щоб задати множину, потрібно вказати, які елементи йому належать. Це можна зробити різними способами:

- перерахунком елементів: М={a₁ ,a₂ ,…,a_k };