Курсовая работа: Доведення теоретико-математичних тотожностей і тверджень

3

4

Блок 1 :використовуємо ProcedureSYS ,яка описана в лабораторній pоботі №1.

Блок 2,3 : не відсортовані масиви; відсортовані масиви.

Блок 4: алгоритм OBED

Алгоритм OBED :

Призначений для об ’ єднання двох відсортованих множин А і В з використанням методу злиття.

Крок 1. Присвоїти , j=1,;

Крок 2. Перевірити умову : якщо так, то: к=к+1,с= ,і=і+1;

Крок 3 . Перевірити умову ; якщо так, то перехід на крок 2;

інакше: записати в кінці масиву С елементи масиву В,

які залишились нерозглянуті; кінець.

Якщо ,то перехід на крок 4 ;

Крок 4. Перевірити ;якщо так, то: к=к+1, с=b,j=j+1

Крок 5. Перевірити умову j; якщо так, то перехід на крок 2 ;

інакше: записати в кінці масива С елементи А, які залишились нерозглянуті; кінець.

Крок 6. ,к=к+1; с=,і=і+1, J=j+1 ;

Крок 7. Провірити умову: о r ( Чи існують іще нерозглянуті елементи множини А чи В);якщо так, то перехід на крок 2 . Інакше : якщо і>n і j<m, то записати в кінці масиву С елементи В, які не були розглянені; кінець .якщо і <nij >m, то записати в кінці масиву С елементи А , які залишились ерозглянуті.Ki нець

2.5.2.4. Блок-схема.

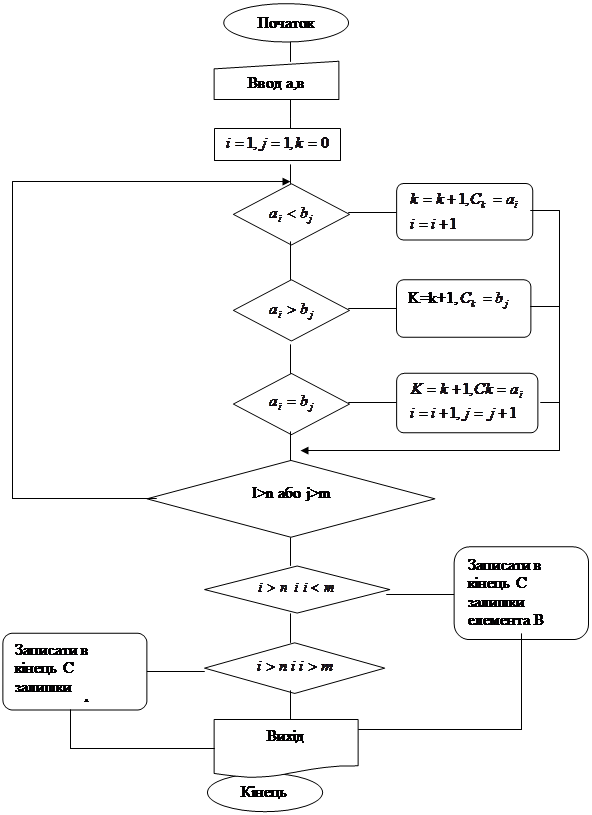
Мал.3. Блок-схема процедури OBED

2.5.3. Опис процедури PERET

2.5.3.1. Постановка задачі.

Задані дві множини: A={а,а,..,а}

В={b,b,..,b}, які упорядковані.

Потрібно отримати множину С=А ÇB

2. 5.3.2. Математична модель

Перетин визначається наступним чином С=А ÇВ={С,СА і СВ}

2.5.3.4. Алгоритм вирішення задачі