Курсовая работа: Доведення теоретико-математичних тотожностей і тверджень

На кожному кроці основного циклу можлива одна з трьох ситуацій: поточний елемент множини А менше, чи більше, чи дорівнює поточному елементу множини В.

· у першому випадку поточний елемент множини А не належить перетинанню, він пропускається і відбувається просування в цій множині;

· у другому випадку теж саме виконується з множиною ;

· у третьому випадку знайдені співпадаючі елементи, один екземпляр елементу додається в результат і відбувається просування відразу в обох множинах.

Алгоритм перетину:

Призначений для перетину двох відсортованих множин А і В з використанням методу злиття.

Крок 0. Ініціалізація: задання множин А і В:

А={а},;

В={b},;

Присвоїти , j =1

Крок 1. Перевірити . Якщо так, то: і=і+1. Перехід на Крок4.

Крок 3. Перевірити ,якщо так, то: j=j+1. Перехід на Крок 4.

Крок 4 . Виконати Крок2 і Крок3 при ( )оr( ) .

Крок 5. Кінець.

Блок-схема .

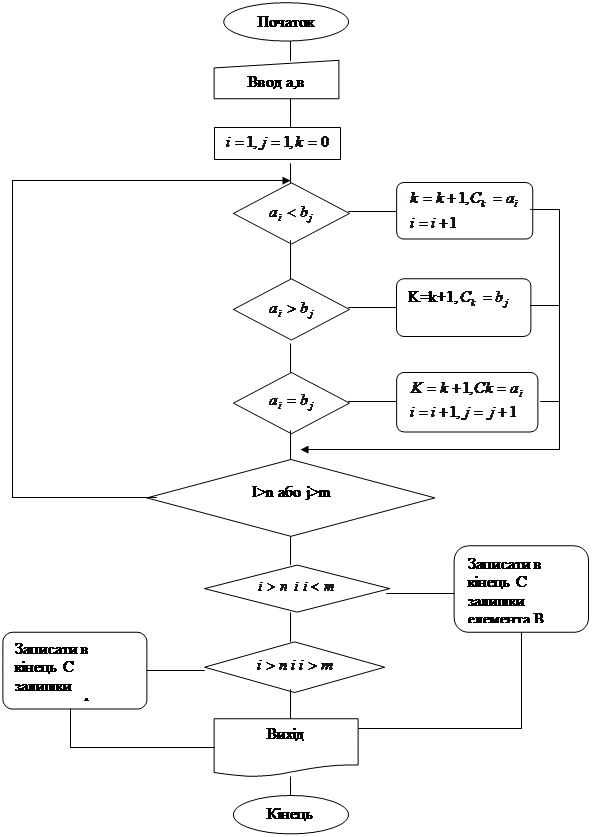
Мал.3. Блок-схема процедури PERET

2.5.4. Опис процедури RIZ .

2.5.4.1. Постановка задачі

Задані дві множини A={а,а,..,а} і В={b,b,..,b}, які упорядковані.

Потрібно отримати множину С=А \B.

2. 5.4.2. Математична модель

Різниця визначається наступним чином С=А \В={с,сÎА і сÏВ}

2.5.4.3. Алгоритм вирішення задачі

Алгоритм вирішення задачі базується на методі злиття двох множин, тому ми можемо допустити не порушуючи загальності, що множини А і В вже відсортували. Приведемо загальний опис вирішення алгоритму задачі.

На кожному кроці основного циклу можлива одна з трьох ситуацій: поточний елемент множини А менше, чи більше, чи дорівнює поточному елементу множини В.

· у першому випадку поточний елемент множини А записується в результат С і розглядається наступний елемент множини А;

· у другому випадку поточний елемент множини А не належить різниці і розглядається наступний елемент множини В;

· у третьому випадку поточний елемент А не належить результату і розглядаються наступні елементи множин А і В.