Курсовая работа: Движение тела под действием силы тяжести

Разложим силу тяготения на две составляющие, одна из которых будет, т.е.

Из уравнений (1) и (2) видим, что

Таким образом, сила тяжести - одна из составляющих силы тяготения, вторая составляющая сообщает телу центростремительное ускорение. В точке Μ на географической широте φ сила тяжести направлена не по радиусу Земли, а под некоторым углом α к нему. Сила тяжести направлена по, так называемой, отвесной прямой (по вертикали вниз).

Сила тяжести равна по модулю и направлению силе тяготения только на полюсах. На экваторе они совпадают по направлению, а по модулю отличие наибольшее.

где ω — угловая скорость вращения Земли, R — радиус Земли.

рад/с,ω = 0,727·10^-4 рад/с.

Так как ω очень мала, то F_T ≈ F. Следовательно, сила тяжести мало отличается по модулю от силы тяготения, поэтому данным различием часто можно пренебречь.

Тогда F_T ≈ F,

Из этой формулы видно, что ускорение свободного падения g не зависит от массы падающего тела, но зависит от высоты.

Если M – масса Земли, R_З – ее радиус, m – масса данного тела, то сила тяжести равна

где g – ускорение свободного падения у поверхности Земли:

Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения. Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81м/с² . Зная ускорение свободного падения и радиус Земли

(R_З = 6,38·10⁶ м), можно вычислить массу Земли M:

При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли. Рисунок иллюстрирует изменение силы тяготения, действующей на космонавта в космическом корабле при его удалении от Земли. Сила, с которой космонавт притягивается к Земле вблизи ее поверхности, принята равной 700 Н.

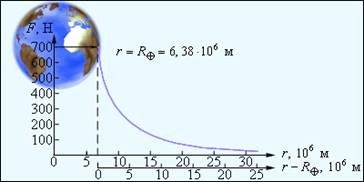
Рис.3.Изменение силы тяготения, действующей на космонавта при удалении от Земли.

Примером системы двух взаимодействующих тел может служить система Земля–Луна. Луна находится от Земли на расстоянии r_Л = 3,84·10⁶ м. Это расстояние приблизительно в 60 раз превышает радиус Земли R_З . Следовательно, ускорение свободного а_л , обусловленное земным притяжением, на орбите Луны составляет

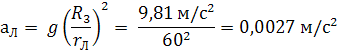
С таким ускорением, направленным к центру Земли, Луна движется по орбите. Следовательно, это ускорение является центростремительным ускорением. Его можно рассчитать по кинематической формуле для центростремительного ускорения:

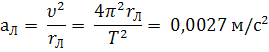
где T = 27,3 сут. – период обращения Луны вокруг Земли. Совпадение результатов расчетов, выполненных разными способами, подтверждает предположение Ньютона о единой природе силы, удерживающей Луну на орбите, и силы тяжести. Собственное гравитационное поле Луны определяет ускорение свободного падения g_л на ее поверхности. Масса Луны в 81 раз меньше массы Земли, а ее радиус приблизительно в 3,7 раза меньше радиуса Земли. Поэтому ускорение g_л определится выражением:

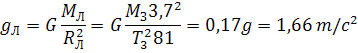
В условиях такой слабой гравитации оказались космонавты, высадившиеся на Луне. Человек в таких условиях может совершать гигантские прыжки. Например, если человек в земных условиях подпрыгивает на высоту 1 м, то на Луне он мог бы подпрыгнуть на высоту более 6 м.