Курсовая работа: Движение тела под действием силы тяжести

Это силы разной природы: сила тяжести — гравитационная сила, вес — упругая сила (электромагнитной природы).

Они приложены к разным телам: сила тяжести — к телу, вес — к опоре.

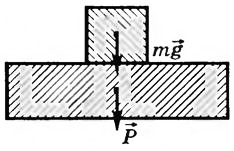
Рис.5. Точки приложения силы тяжести и веса тела.

Направление веса тела не обязательно совпадает с отвесным направлением.

Сила тяжести тела в данном месте Земли постоянная и не зависит от характера движения тела; вес зависит от ускорения, с которым движется тело.

Рассмотрим, как изменяется вес тела, движущегося в вертикальном направлении вместе с опорой. На тело действуют сила тяжести и сила реакции опоры.

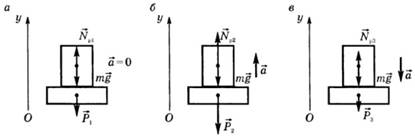
Рис.5. Изменение веса тела при движении с ускорением.

Основное уравнение динамики: . В проекции на ось Оу:

а) .

По третьему закону Ньютона модули сил N_p1 = P₁ . Следовательно, вес тела P₁ = mg

б)

Значит

, (тело испытывает перегрузки).

в)

Следовательно, вес тела

Если a = g, то P = 0

Таким образом, вес тела при вертикальном движении может быть в общем случае выражен формулой

Мысленно разобьем неподвижное тело на горизонтальные слои. На каждый из этих слоев действует сила тяжести и вес вышележащей части тела. Этот вес будет становиться тем больше, чем ниже лежит слой. Поэтому под влиянием веса вышележащих частей тела каждый слой деформируется и в нем возникают упругие напряжения, которые возрастают по мере перехода от верхней части тела к нижней.

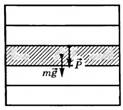
Рис.6.Тело, разбитое на горизонтальные слои.

Если тело свободно падает (a = g), то его вес равен нулю, в теле исчезают всякие деформации и, несмотря на сохраняющееся действие силы тяжести, верхние слои не будут давить на нижние.

Состояние, при котором в свободно движущемся теле исчезают деформации и взаимные давления, называется невесомостью. Причина невесомости заключается в том, что сила всемирного тяготения сообщает телу и его опоре одинаковое ускорение.

1.3 Движение тела, если начальная скорость направлена под углом к силе тяжести

Тело брошено горизонтально, т.е. под прямым углом к направлению силы тяжести.

При этом v_0x = v₀ , g_x = 0, v_0y = 0, g_y = - g , х₀ = 0, и, следовательно,