Курсовая работа: Емкость резкого p-n перехода
N(E)dE=![]() (2m)
(2m)![]() e
e![]() E
E![]() dE
dE
dn=![]() (2m
(2m![]() )
)![]() e
e![]() e
e![]() E
E![]() dE
dE
где m – эффективная масса электронов, располагающихся у дна зоны проводимости.
Обозначим расстояние от дна зоны проводимости до уровня Ферми через -m, а от уровня Ферми до потолка валентной зоны через -m¢. Из рис. 1 видно, что
m+m¢=-E![]() ,
,
m¢=-(Е![]() +m)
+m)
где Е![]() (
(![]() Е) - ширина запрещенной зоны.
Е) - ширина запрещенной зоны.
E![]() =Е +bТ
=Е +bТ
Полное число электронов n, находящихся при температуре Т в зоне проводимости, получим, интегрируя (1.2) по всем энергиям зоны проводимости, т.е. в пределах от 0 до Е![]() :
:
n=4![]()
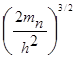
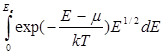
Так как с ростом Е функция exp(-E/kT) спадает очень быстро, то верхний предел можно заменить на бесконечность:
n=4![]()
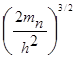
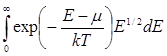
Вычисление этого интеграла приводит к следующему результату:
n=2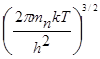 exp
exp![]() (1.5)
(1.5)
Введем обозначение
N![]() =2(2
=2(2![]() m
m![]() kT/h
kT/h![]() )
)![]() (1.6)
(1.6)
Тогда (1.5) примет следующий вид:
n=N![]() exp(
exp(![]() /kT) (1.7)
/kT) (1.7)
Множитель N![]() в (1.7) называют эффективным числом состояний в зоне проводимости, приведенным ко дну зоны. Смысл этого числа состоит в следующем. Если с дном зоны проводимости, для которой Е=0, совместить N
в (1.7) называют эффективным числом состояний в зоне проводимости, приведенным ко дну зоны. Смысл этого числа состоит в следующем. Если с дном зоны проводимости, для которой Е=0, совместить N![]() состояний, то, умножив это число на вероятность заполнения дна зоны, равную f
состояний, то, умножив это число на вероятность заполнения дна зоны, равную f![]() (0)=exp(
(0)=exp(![]() /kT), получим концентрацию электронов в этой зоне.
/kT), получим концентрацию электронов в этой зоне.
Подобный расчет, проведенный для дырок, возникающих в валентной зоне, приводит к выражению:
p=2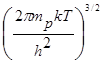 exp
exp![]() =N
=N![]() exp
exp![]() = N
= N![]() exp
exp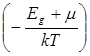 (1.8)
(1.8)
где
N![]() =2
=2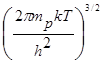 (1.9)
(1.9)
– эффективное число состояний в валентной зоне, приведенное к потолку зоны.
Из формул (1.7) и (1.8) следует, что концентрация свободных носителей заряда в данной зоне определяется расстоянием этой зоны от уровня Ферми: чем больше это расстояние, тем ниже концентрация носителей, так как m и m¢ отрицательны.
В собственных полупроводниках концентрация электронов в зоне проводимости n![]() равна концентрации дырок в валентной зоне p
равна концентрации дырок в валентной зоне p![]() , так как
, так как
каждый электрон, переходящий в зону проводимости, «оставляет» в валентной зоне после своего ухода дырку. Приравнивая правые части соотношения (1.5) и (1.8), находим
2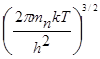 exp
exp![]() =2
=2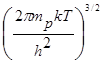 exp
exp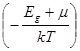
Решая это уравнение относительно m, получаем
m![]() = -
= -![]() +
+![]() kTln
kTln![]() (1.10)
(1.10)