Курсовая работа: Емкость резкого p-n перехода
n![]() =p
=p![]() =2
=2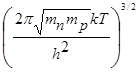 exp
exp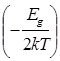 =(N
=(N![]() N
N![]() )
)![]() exp
exp (1.11)
(1.11)
Из формулы (6.12) видно, что равновесная концентрация носителей заряда в собственном полупроводнике определяется шириной запрещенной зоны и температурой. Причем зависимость n![]() и p
и p![]() от этих параметров является очень резкой.
от этих параметров является очень резкой.
Рассчитаем собственную концентрацию электронов и дырок при Т=300К.
Eg =(0,782-3,9![]() 10
10![]()
![]() 300)1,6 10-19 =1,064
300)1,6 10-19 =1,064![]() 10-19 Дж
10-19 Дж
N![]() =2(2
=2(2![]() m
m![]() kT/h
kT/h![]() )
)![]() =2
=2 =2
=2![]() = =2
= =2![]() =4,7
=4,7![]() 10
10![]() (см
(см![]() )
)
N![]() =2
=2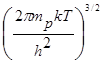 =2
=2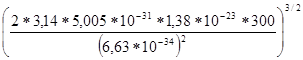 =2
=2![]() =10,2
=10,2![]() 10
10![]() (см
(см![]() )
)
n![]() =p
=p![]() =(N
=(N![]() N
N![]() )
)![]() exp
exp![]() =
=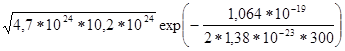 =
=
6,92![]() 10
10![]()
![]() 2
2![]() 10
10![]() =13,8
=13,8![]() 10
10![]() (см
(см![]() )
)
2. Расчет контактной разности потенциалов
Для n-области основными носителями являются электроны, для p-области – дырки. Основные носители возникают почти целиком вследствие ионизации донорных и акцепторных примесей. При не слишком низких температурах эти примеси ионизированы практически полностью, вследствие чего концентрацию электронов в n-области n![]() можно считать равной концентрации донорных атомов: n
можно считать равной концентрации донорных атомов: n![]() »N
»N![]() , а концентрацию дырок в p-области p
, а концентрацию дырок в p-области p![]() – концентрация акцепторных атомов в p-области: p
– концентрация акцепторных атомов в p-области: p![]() »N
»N![]() .
.
Помимо основных носителей эти области содержат не основные носители: n-область – дырки (p![]() ), p-область – электроны (n
), p-область – электроны (n![]() ). Их концентрацию можно определить, пользуясь законом действующих масс:
). Их концентрацию можно определить, пользуясь законом действующих масс:
n![]() p
p![]() = p
= p![]() n
n![]() =n
=n![]() .
.
Как видим, концентрация дырок в p-области на 6 порядков выше концентрации их в n-области, точно так же концентрация электронов в n-области на 6 порядков выше их концентрации в p-области. Такое различие в концентрации однотипных носителей в контактирующих областях полупроводника приводит к возникновению диффузионных потоков электронов из n-области в p-область и дырок из p-области в n-область. При этом электроны, перешедшие из n- в p-область, рекомбинируют вблизи границы раздела этих областей с дырками p-области, точно так же дырки, перешедшие из p- в n-область, рекомбинируют здесьс электронами этой области. В результате этого в приконтактном слое n-области практически не остается свободных электронов и в нем формируется неподвижный объемный положительный заряд ионизированных доноров. В приконтактном слое p-области практически не остается дырок и в нем формируется неподвижный объемный отрицательный заряд ионизированных акцепторов.
Неподвижные объемные заряды создают в p–n-переходе контактное электрическое поле с разностью потенциалов V![]() , локализованное в области перехода и практически не выходящее за его пределы. Поэтому вне этого слоя, где поля нет, свободные носители заряда движутся по-прежнему хаотично и число носителей, ежесекундно наталкивающихся на слой объемного заряда, зависит только от их концентрации и скорости теплового движения. Как следует из кинетической теории газов, для частиц, подчиняющихся классической статистике Максвела–Больцмана, это число nопределяется следующим соотношением:
, локализованное в области перехода и практически не выходящее за его пределы. Поэтому вне этого слоя, где поля нет, свободные носители заряда движутся по-прежнему хаотично и число носителей, ежесекундно наталкивающихся на слой объемного заряда, зависит только от их концентрации и скорости теплового движения. Как следует из кинетической теории газов, для частиц, подчиняющихся классической статистике Максвела–Больцмана, это число nопределяется следующим соотношением:
n=![]() n
n![]() S, (2.1)
S, (2.1)
где n![]() - концентрация частиц;
- концентрация частиц;![]() - средняя скорость теплового движения; S – площадь, на которую они падают.
- средняя скорость теплового движения; S – площадь, на которую они падают.
Неосновные носители – электроны из p-области и дырки из n-области, попадая в слой объемного заряда, подхватываются контактным полем V![]() и переносятся через p–n-переход.
и переносятся через p–n-переход.
Обозначим поток электронов, переходящих из p- в n-область, через n![]() , поток дырок, переходящих из n- в p-область, через p
, поток дырок, переходящих из n- в p-область, через p![]() .
.
Согласно (2.1) имеем
n![]() =
=![]() n
n![]()
![]()
![]() S, (2.2)
S, (2.2)
p![]() =
=![]() p
p![]()
![]()
![]() S. (2.3)
S. (2.3)
Иные условия складываются для основных носителей. При переходе из одной области в другую они должны преодолевать потенциальный барьер высотой qV![]() , сформировавшийся в p–n-переходе. Для этого они должны обладать кинетической энергией движения вдоль оси c, не меньшей qV
, сформировавшийся в p–n-переходе. Для этого они должны обладать кинетической энергией движения вдоль оси c, не меньшей qV![]() . Согласно (2.1) к p–n-переходу подходят следующие потоки основных носителей:
. Согласно (2.1) к p–n-переходу подходят следующие потоки основных носителей:
n![]() =
=![]() n
n![]()
![]()
![]() S,
S,
p![]() =
=![]() p
p![]()
![]()
![]() S.
S.
В соответствии с законом Больцмана преодолеть потенциальный барьер qV![]() сможет только n
сможет только n![]() exp (-qV
exp (-qV![]() /kT) электронов и p
/kT) электронов и p![]() exp (-qV
exp (-qV![]() /kT) дырок. Поэтому потоки основных носителей, проходящие через p–n-переход, равны
/kT) дырок. Поэтому потоки основных носителей, проходящие через p–n-переход, равны
n![]() =
=![]() n
n![]()
![]()
![]() exp (-qV
exp (-qV![]() /kT), (2.4)
/kT), (2.4)
p![]() =
=![]() p
p![]()
![]()
![]() exp (-qV
exp (-qV![]() /kT), (2.5)
/kT), (2.5)
На первых порах после мысленного приведения n- и p-областей в контакт потоки основных носителей значительно превосходят потоки неосновных носителей: n![]() >>n
>>n![]() , p
, p![]() >>p
>>p![]() . Но по мере роста объемного заряда увеличивается потенциальный барьер p–n-перехода qV
. Но по мере роста объемного заряда увеличивается потенциальный барьер p–n-перехода qV![]() и потоки основных носителей согласно (2.4) и (2.5) резко уменьшаются. В то же время потоки неосновных носителей, не зависящие от qV
и потоки основных носителей согласно (2.4) и (2.5) резко уменьшаются. В то же время потоки неосновных носителей, не зависящие от qV![]() [ см. (2.2) и (2.3)] остаются неизменными. Поэтому относительно быстро потенциальный барьер достигает такой высоты j
[ см. (2.2) и (2.3)] остаются неизменными. Поэтому относительно быстро потенциальный барьер достигает такой высоты j![]() = qV
= qV![]() , при которой потоки основных носителей сравниваются с потоками неосновных носителей:
, при которой потоки основных носителей сравниваются с потоками неосновных носителей:
n![]() =n
=n![]() , (2.6)
, (2.6)
p![]() =p
=p![]() . (2.7)
. (2.7)