Курсовая работа: Энергетический и кинематический расчет привода

d_b1 = d₁ *cos _t = 140*cos 200 = 132 мм;

d_b2 = d₂ *cos _t = 140*cos 200 = 132 мм;

где d₁ , d₂ – делительный диаметр шестерни и колеса;

_t – торцовый угол профиля;

Далее определяем диаметр вершин зубъев шестерни и диаметр вершин зубъев колеса по выражениям:

d_a1 = d₁ +2*m*(h_a ^* +x₁ ) = 140+2*7*(1+0,5) = 161 мм

d_a2 = d₂ +2*m*(h_a ^* +x₂ ) = 476+2*7*(1+0,5) = 497 мм

где d₁ , d₂ – делительный диаметр шестерни и колеса;

x₁ , x₂ – коэффициенты смещения шестерни и колеса;

Затем определяем диаметр впадин зубъев шестерни и колеса по выражениям:

d_{f 1} = d₁ – 2*m*(h_f ^* - x₁ ) = 140-2*7(1,25-0,5) = 129 мм

d_{f 2} = d₂ – 2*m*(h_f ^* - x₂ ) = 476-2*7(1,25-0,5) = 465 мм

Находим коэффициент наименьшего смещения шестерни x_min , x_min = -0,2. Должно выполняться условие x_min <= x₁ ;

-0,2 <= 0,5 – условие выполняется.

Определяем основной угол наклона по выражению:

₆ =arcsin(sin *cos ) = 0⁰ ;

Далее находим основной окружной шаг и осевой шаг по выражениям:

P_{6 t} = *m*cos _t / cos 3,14*7*cos 20/cos 0 = 21 мм;

P_x = *m/ sin 3,14*7/sin 0 = 0 мм;

где m – модуль;

 - угол наклонения зуба;

_t – торцовый угол профиля;

Вычисляем угол профиля зуба шестерни в точке на окружности вершин _{a 1} , _{a 1} = 35⁰ .

Определяем угол профиля зуба колеса в точке на окружности вершин _{a 2} , _{a 2} = 26⁰ .

Затем определяем коэффициент торцового перекрытия и коэффициент осевого перекрытия _ и _ , _ = 1,65, _ = 0.

Определим суммарную длину контактных линий по формуле:

l_m =b_ *_ /cos _t = 181 мм;

Вычисляем коэффициент среднего изменения суммарной длины контактных линий по формуле:

;
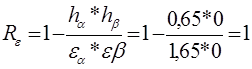