Курсовая работа: Фізика відкритих систем. Синергетика

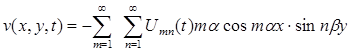
Далі, можна підставити вираження (3.8) у рівняння (3.4) і, використовуючи співвідношення ортогональності для базисних функцій, одержати систему рівнянь.

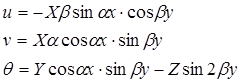(3.9)

Прирівнюючи коефіцієнти в лівій і правій частині, одержуємо:

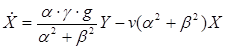(3.10)

Із другим рівнянням поступаємо аналогічно. Різниця, однак, у тім, що в лівій частині тепер присутні дві просторові моди – комбінації косинусів та синусів:

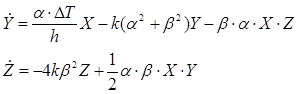(3.11)

Отже, ми знайшли систему трьох звичайних диференціальних рівнянь для динамічних змінних X, Y, Z. Щоб з нею було зручно працювати, корисно привести рівняння до безрозмірного виду за допомогою деякої заміни змінних і параметрів. Підставимо в (3.10)-(3.11) X = Ах, Y = Ву, Z = Cz, t = Dτ, де А, В, C, D- деякі постійні коефіцієнти. Тоді отримуємо:

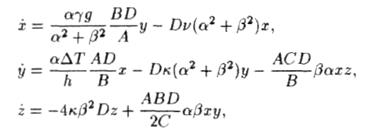(3.12)

Спробуємо підібрати коефіцієнти так, щоб вид рівнянь максимально спростився.

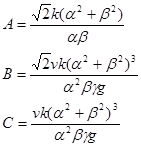(3.13)

Крім того введемо безрозмірні параметри:

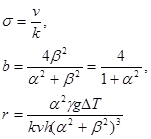(3.14)

Тоді рівняння (3.12) матимуть вигляд:

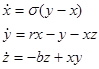(3.15)

Це і є модель Лоренцо (3.15). Вона являє собою динамічну систему із тривимірним фазовим простором. Миттєвий стан визначається набором трьох змінних (х, y, z), а оператор еволюції визначений конкретним видом рівнянь (3.15). Змінна х характеризує швидкість обертання конвекційних валів, величини y и z відповідають за розподіл температури, відповідно, по горизонталі й по вертикалі. Параметр b визначається геометрією конвекційного осередку, а саме, відношенням її вертикального й горизонтального розмірів а. Параметр є відношення коефіцієнта кінематичної в'язкості й коефіцієнта температуропровідності v/k. Його називають числом Прандтля. Комбінацію називають числом Рєлея. У свій час Рєлей показав, що умові виникнення конвекційного ходу у вигляді валів відповідає певне критичне значення цього числа, а саме, . З формули (3.10) видно, що параметр г являє собою відношення .

Розділ 4. Фрактальні структури й розмірність дивних атракторів

Дисипативні динамічні системи володіють тією властивістю, що їх розв’язки при притягуються до деякої підмножини міри нуль у фазовому просторі. Ця підмножина для випадку регулярної динаміки може бути або стійкою стаціонарною точкою, або стійким граничним циклом, або інваріантним тором. Всі ці підмножини є підмножинами фазового простору. Математичним вираженням хаотичних коливань дисипативних систем служить дивний атрактор, який уже не володіє гладкою структурою й достатньою безперервністю. Геометрична будова дивних атракторів більш складна. Вони володіють геометричною {масштабною) інваріантністю, або, як іноді говорять, скейлинговою структурою.

Щоб краще уявити собі, про що йде мова, розглянемо характерний приклад – атрактор Ено, що виникає в простій моделі, яка описується точковим відображенням Ено.

Ми вже знаємо, що дивні атракторы можуть з'являтися в системах диференціальних рівнянь, розмірність фазового простору яких більше або рівна трьом, . Однак складні геометричні притягаючі множини, можуть виникати й у так званих точкових відображеннях – динамічних системах з дискретним часом. Використовуючи точкові відображення, можна описувати системи самої різної природи – від фізичної до біологічної. Відображення Ено – це оборотне двовимірне точкове відображення, яке в принципі можна розглядати як відображення Пуанкаре для деякої двомірної січної поверхні і трьохмірного потоку.

Розглянемо в п-мірному фазовому просторі динамічної системи деяку множину А. Покриємо дану множину п-мірними кубиками зі стороною а так, щоб ці кубики містили всі точки множини сили А. Нехай N – мінімальне число кубиків, необхідних для покриття А. Розглянемо межу

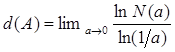(4.1)

Величина є метричною розмірністю й називається ємністю або фрактальною розмірністю (5). Зауважимо, що в літературі ємність іноді називають також хаусдорфовою або ентропійною розмірністю.

Для регулярних сил (наприклад, шматка тривимірного евклідового простору, поверхні або лінії) фрактальна розмірність дорівнює цілому числу (відповідно 3, 2, 1) і співпадає зі звичайною розмірністю. Дійсно, при малих а з (4.1) одержуємо:

(4.2)

Однак для нерегулярних сил, що володіють масштабно-інваріантною структурою, фрактальная розмірність має дробове значення.

Визначимо спочатку фрактальную розмірність множин, які ми розглянули раніше, множини середніх третин і килима Серпиньського.

З побудови сил середніх третин витікає, що вони

Рис. 4. Побудова множини Кантора. складаються із розділених інтервалів довжиною кожний. Справді, при к=0 N=1, a=1. Якщо к=1, то N=2, a=1/3, для к=2, N=4, a=1/9 і для k = m і (рис. 4).

Тут к означає число ітерацій побудови сил. Отже, використавши формулу (4.1), одержимо: