Курсовая работа: Идентификация технологических объектов управления
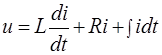
Или
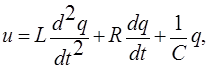
где q — заряд; R, L, С - активное сопротивление резистора, индуктивность катушки и емкость конденсатора, включенных в цепь;
механическая цепь:
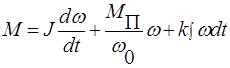
или
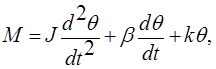
где J — момент инерции;
θ,ω — угол и угловая скорость двигателя;
β = Мп /ω0 — жесткость механической характеристики двигателя;
к = M/a — жесткость кинематического звена. Второе слагаемое второго уравнения момента характеризует суммарный момент сопротивления Мс.
Элементы, связанные соединениями, в которых не происходит накопления и преобразования вещества или энергии, образуют структуру системы, отражающую технологический процесс преобразования этих видов продуктов. Для анализа такой структуры используются два закона: сумма расходов продукта в любом разветвлении равна 0:
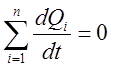
сумма разностей уровней потенциалов в любом контуре равна 0:
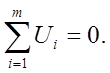 (3.2)
(3.2)
Решение уравнений типа (3.2) и (3.3) может дать принципиально разные результаты.
Если многоконтурная система имеет один вход и один выход, то система дифференциальных уравнений первого порядка, описывающих процессы в элементах, даст дифференциальное уравнение, порядок которого определяется числом накопителей энергии в системе.
Технологические объекты управления, как правило, являются многосвязными системами, имеющими несколько входов и выходов. Для них характерна зависимость каждого выхода от всех входов системы. Математическая модель такой системы представляет собой систему дифференциальных уравнений различного порядка, в левой части каждого из этих уравнений фигурирует одна из выходных переменных, а в правой — все входные. Для анализа подобных систем их математические модели обычно представляют в матричной форме.
Модели многосвязных систем
Для современных АСУ ТП характерно объединение в единую систему отдельных приводов и механизмов и даже объединение сложных технологических агрегатов в комплексно-автоматизированные технологические линии, гибкие автоматизированные производства. Примерами первых могут служить станки с ЧПУ, отрабатывающие при обработке детали сложные траектории и обеспечивающие оптимальный режим резания; примерами вторых — технологические линии прокатного производства. Основной особенностью таких систем является невозможность рассмотрения их как механической совокупности от дельных механизмов. Это обусловлено взаимосвязью и взаимовлиянием друг на друга управляемых технологических параметров.
Для обеспечения требуемого качества продукции необходимо одно временно управлять многими взаимосвязанными переменными (технологическими параметрами) путем непрерывного воздействия на различные исполнительные механизмы. В подобных системах изменение одного управляющего или возмущающего воздействия вызывает изменение нескольких управляемых переменных и наоборот - каждая управляемая переменная зависит от нескольких управляющих воз действий. Многосвязными являются большинство систем, у которых есть несколько возможностей управлять одним объектом, подверженным обычно нескольким внешним воздействиям. Подобные системы называют также многоканальными или многомерными.
В многоканальных системах в отличие от одноканальных входные воздействия и выходы объекта в каждый момент времени описываются как многомерные векторы, а сам объект — оператором А, пре образующим вектор входных воздействий X в вектор выходных переменных Y:
Y = АX. (3.4)
В этом случае можно говорить об аналогии между оператором А и передаточной функцией в одноканальных системах. В многоканальных системах решаются те же задачи, что и в одноканальных, т.е стабилизация, программное и следящее управление, оптимизация. Здесь также решается вопрос об устойчивости системы, качестве ее динамики. Представляя систему многомерной, необходимо уметь путем структурных преобразований упрощать внутреннюю структуру сложной системы, соединять ее с другими системами и т.д. Самостоятельной задачей является получение и представление формализованных моделей таких систем.
Основным физическим принципом, положенным в основу аналитических методов получения моделей многомерных объектов, является метод универсальных уравнений.
Записав уравнения по типу (3.2), получим, например, для установившегося режима трехсвязной линейной системы уравнения вида:
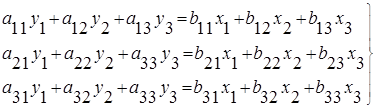 (3.5)
(3.5)
где х1 ,х2 ,х3 – входные, а у1 ,у2 ,у3 – выходные переменные; aij , bij – коэффициенты – вещественные числа, которые могут принимать также и нулевые значения.