Курсовая работа: Идентификация технологических объектов управления

Оптимальной может считаться модель, у которой при определенных расчетом коэффициентах сумма квадратов отклонений расчетных ур и экспериментальных у_э значений будет минимальной, т.е. минимизируется функционал

где п — число опытов.

Для определения коэффициентов модели составляют систему уравнений типа

Совместное решение полученных уравнений относительно a_i дает такие их значения, при которых удовлетворяется условие (3.15).

Для упрощения (3.16) целесообразно начало отсчета абсциссы x_i помещать в середину интервала экспериментально снятых значений и пользоваться симметричными значениями x_i (одинаковыми, но раз личными по знакам). В этом случае все суммы нечетных степеней х будут обращаться в нуль, что существенно упростит систему уравнений.

Например, если в качестве модели выбран полином второй степени

то функционал (3.15) имеет вид

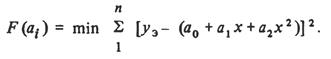
Коэффициенты являются неизвестными переменными. В соответствии с (3.16) составляем систему уравнений:

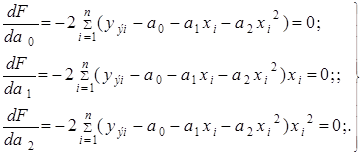
Приравнивая суммы нечетных степеней x_i к нулю, получаем

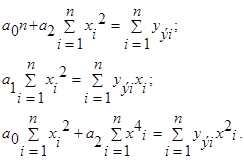
Решение относительно коэффициентов:

Рассчитав коэффициенты и подставив их в (3.16), получим уравнение регрессии.

Идентификация многомерных объектов

Получение модели многомерных объектов по результатам эксперимента осложняется прежде всего тем, что на исследуемый параметр влияет много факторов, которые сложно разделить на существенные и несущественные, поэтому трудно определить число входов объекта, подлежащих учету.

В отличие от одномерных объектов затруднена геометрическая интерпретация модели. Так, для двух входных параметров, влияющих на третий выходной, приходится обращаться к двухмерной области. Увеличение входов требует рассмотрения многомерной гиперповерхности, описываемой уравнением с несколькими аргументами и не поддающейся геометрической интерпретации.

Вместе с тем модель, отражающая зависимость исследуемого параметра или критерия от многих переменных, должна быть достаточно информативной, достоверной и удобной в пользовании.

При значительном числе входов x_i модель может быть нелинейной и иметь сложный рельеф с вершинами, впадинами, гребнями. Поиск экстремальных точек (вершин и впадин) на этой поверхности путем изменения входных величин составляет содержание оптимального управления. Обычно такая модель называется целевой функцией или поверхностью отклика, а оптимальное управление обеспечивает работу технологического объекта управления в области экстремального значения критерия качества.

Получить по данным эксперимента модель объекта управления, точно воспроизводящую поверхность отклика, весьма сложно. Поэтому на практике часто ограничиваются ее линейным или квадратичным приближением, выбирая диапазон изменения переменных в ограниченной области. Это возможно, если функция непрерывная и выпуклая. Границы области обычно выбирают так, чтобы в нее попал экстремум или предельно допустимые значения yи x_i .

Такой подход может дать в большей степени качественное, нежели количественное решение. Оно сводится к оценке влияния различных факторов на исследуемую переменную y и дает возможность пренебречь некоторыми из них.

Метод, позволяющий получить многомерную модель объекта управления на основе эксперимента, получил название факторного анализа, нередко он называется методом планирования эксперимента, факторным экспериментом и т.п. Применительно к детерминированному объекту метод заключается в следующем:

- для объекта выбирают факторы х_i , оказывающие существенное влияние на выход у; определяют области изменения х_i ;

- составляют программу (план) эксперимента;

- принудительно изменяя x_i в избранных пределах и сочетаниях, определяемых программой эксперимента, фиксируют значения у;