Курсовая работа: Идентификация технологических объектов управления

или в матричной форме

или, если раскрыть матрицы

Здесь Y(f) - столбец неизвестных выходных функций времени или переменных состояния; F (t) — столбец задающих (входных) функций времени; А, В — квадратные матрицы постоянных коэффициентов.

Сравнивая (3.14) с записью дифференциального уравнения первого порядка и располагая формулой его решения

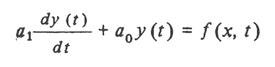
И располагая формулой его решения

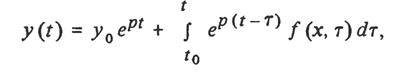
где τ — переменная интегрирования, можно доказать, что и для матричного выражения системы дифференциальных уравнений можно напирать аналогичное выражение для ее решения. Здесь матричная экспоненциальная функция е^At может быть представлена рядом системы уравнения вида:

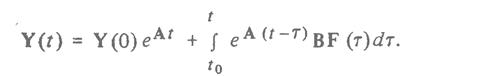
Здесь матричная экспоненциальная функция е^At может быть представлена рядом:

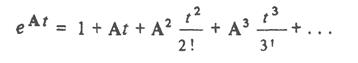
Требуемые для получения временных функций суммирование и умножение матриц выполняются на ЭВМ по типовым программам.

Как и одномерные системы, многомерные решают задачи стабилизации совокупности параметров, программно-следящего их изменения или оптимизации.

Специфичным для многомерных систем является возможность неравенства числа входов и выходов, обычно п_у ≤ п_х , а также взаимовлияние каналов друг на друга. Формально это взаимовлияние представляется в виде перекрестных связей с передаточными функциями Н₂ (р), Н₆ (р), Н₇ (р) на рис. 3.1. Если они являются объективным проявлением природы управляемого объекта, они называются естественными. Если введены специально, например, для нейтрализации взаимовлияния — искусственными или корректирующими.

Например (рис. 3.1), для компенсации влияния y на y₃ представ ленного в виде естественной связи с передаточной функцией Н₆ (р), необходимо на вход х₆ подать с входа Х корректирующую связь с передаточной функцией

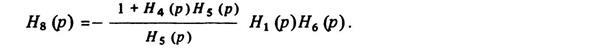
Тогда выражение для у_ъ (р) в (3.8) примет вид

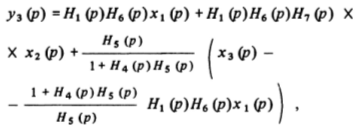
или

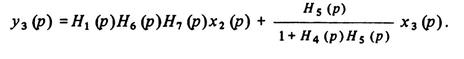
Здесь у_ъ становится независимым от х i.

Рассматривая систему (3.8), можно ввести понятие передаточной матрицы является собственными передаточными функциями. Они отражают зависимость выхода от "своего" входа; остальные (обозначим их L) являются несобственными. Тогда

где

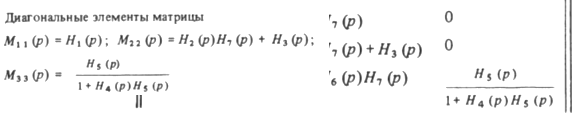
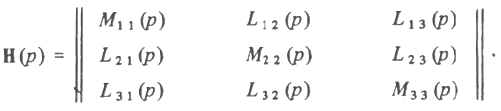
Очевидно, чтобы каналы стали автономными, передаточная матрица должна стать диагональной.