Курсовая работа: Идентификация технологических объектов управления
После решения системы уравнений (3.5) или ее динамического аналога она принемает вид:
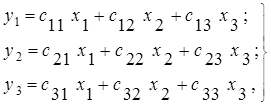 (3.6)
(3.6)
где ci — вещественный коэффициент для уравнений статики или передаточная функция для уравнений динамики.
Модель системы в виде уравнений (3.5) или (3.6) может быть определена любой внутренней структурой, т.е. связи между каналами могут быть обусловлены непосредственным взаимодействием переменных, прямыми связями входа с различными выходами и обратными связями от выходов к входам. На рис. 3.1 приведена система, обладающая указанными свойствами. Эту систему можно описать следующими уравнениями:
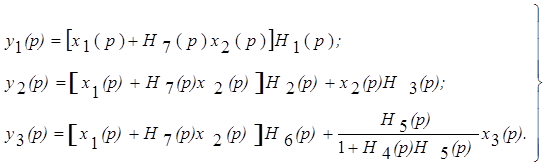
После преобразований система (3.7) принимает вид, аналогичный (3.6):
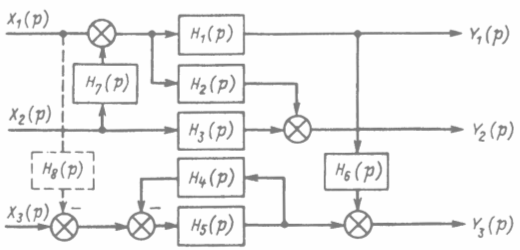
Рисунок 3.1 – Пример трехсвязной структуры
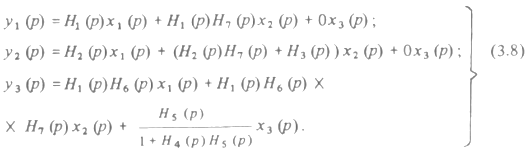
Как видно из изложенного, даже для относительно простой системы запись формальной модели получается весьма громоздкой. После приведения ее к виду (3.6) решать систему обычным способом становится сложно. С увеличением числа входов и выходов задача еще более усложняется.
Для получения более компактных и унифицированных форм представления моделей многомерных систем применяется матричная форма записи переменных и операторов преобразования.
Например, система (3.5) в матричной форме может быть представлена в виде
AY = ВХ, (3.9)
где X, Y - матрицы входных и выходных переменных; А, В - матрицы преобразований.
Система (3.6) принимает вид
Y = СХ. (3.10)
Под матрицами в данном случае понимается упорядоченная, т.е. выполненная по определенному правилу, табличная форма записи цифр, буквенных коэффициентов или передаточных функций и полиномов. Так, в (3.10) матрицы имеют вид:
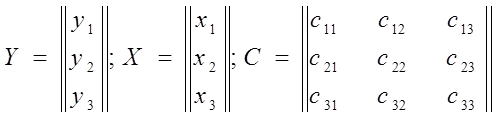
Главное преимущество матричной формы записи заключается в том, что, составляя матрицы по определенным правилам, можно трансформировать в матричную форму не только запись переменных, но и операции над ними.
При наличии некоторых навыков операции над матрицами также легче воспринимаются, чем операции с множеством переменных. Математическое обеспечение современных ЭВМ располагает программами, ориентированными на унифицированное матричное представление задач анализа и синтеза многомерных систем, что позволяет широко применять для этих целей современную вычислительную технику.
Использование матричного представления объекта весьма эффективно при анализе и синтезе системы по динамическим показателям. Одним из наиболее современных методов анализа динамики много мерных систем является метод пространства состояний. Под переменными состояния и образуемым ими пространством состояний понимается совокупность величин, позволяющих по известным входным сигналам для t > t0 определить выходные сигналы для t≥ t0 .
В качестве переменных состояния могут приниматься как выходные переменные, так и их производные. Так, для одномерной системы, описываемой дифференциальным уравнением л-го порядка, переменными состояния будут значения у и (n – 1) производных в момент t = 0, позволяющие в дальнейшем при решении дифференциального уравнения классическим методом определить постоянные интегрирования.
Для многомерной системы понятие переменных состояния рассмотрим на примере электропривода с системой управления преобразователь - двигатель при действии на преобразователь двух управляющих воздействий и1 и и2 . Динамическая модель такой системы имеет вид:
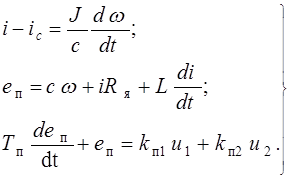 (3.11)
(3.11)
Выберем в качестве переменных состояния интересующие нас величины, приняв их выходами системы, и обозначим их
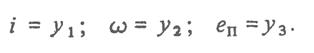
Запишем выражения для динамической модели объекта в виде системы дифференциальных уравнений в канонической форме:
 (3.12)
(3.12)
Применительно к примеру система будет иметь вид: