Курсовая работа: Інформаційно-вимірювальна система для пасажирських вагонів залізничного транспорту

Побудуємо графік залежності вихідної величини від часу рисунок 4.2

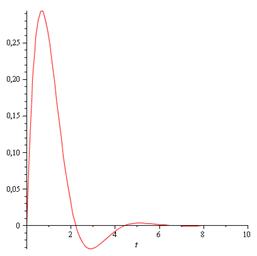
Рисунок 4.6 – Графік залежності вихідної величини від часу

Знайдемо передатну функцію заданого диференціального рівняння

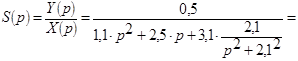
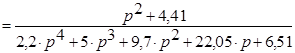. (4.28)

Замінимо оператор Лапласа в передатній функції на та отримаємо комплексну частотну характеристику

. (4.29)

Виділимо дійсну та уявну частини в знаменнику:

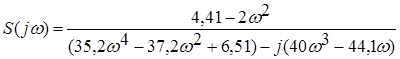. (4.30)

Помножимо чисельник та знаменник дробу на вираз, комплексно спряжений до знаменника, для того, щоб позбутись ірраціональності в знаменнику. В результаті отримаємо

. (4.31)

З даного виразу маємо дійсну

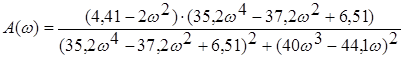(4.32)

та уявну

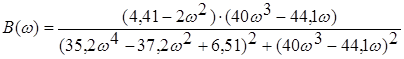. (4.33)

частини комплексної частотної характеристики.

Знайдемо амплітудно-частотну характеристику як корінь із суми піднесених до квадрату дійсної та уявної частин комплексної частотної характеристики:

. (4.34)

Замінимо , тоді

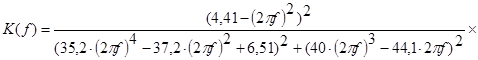
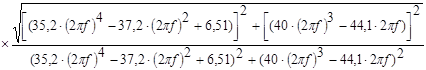(4.35)

Графічно амплітудно-частотну характеристику наведено на рисунку 4.7

Рисунок 4.7 – Амплітудно-частотна характеристика

Знайдемо фазочастотну характеристику як мінус арктангенс відношення уявної частини комплексної частотної характеристики до дійсної

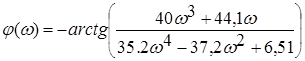. (4.36)

Після заміни отримаємо

. (4.37)