Курсовая работа: Интерполяция функции одной переменной методом Ньютона

. (3)

где , , - степень многочлена.

Максимальное значение равно . Тогда и разделенная разность n-го порядка на участке равна

,

т.е. равна разности разделенных разностей -го порядка, разделенной на длину участка .

Разделенные разности

являются вполне определенными числами, поэтому выражение (1) действительно является алгебраическим многочленом -й степени. При этом в многочлене (1) все разделенные разности определены для участков ,.

При вычислении разделенных разностей принято записывать их в виде таблицы

	•
		•	•	•
■	•	•	•
•	•	•
•	•

Разделенная разность -го порядка следующим образом выражается через значения функции в узлах:

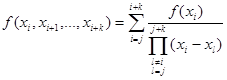. (1)

Эту формулу можно доказать методом индукции. Нам потребуется частный случай формулы (1):

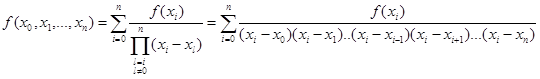
Интерполяционным многочленом Ньютона называется многочлен

Рассмотренная форма полинома Ньютона носит название первой интерполяционной формулы Ньютона, и используется, обычно, при интерполировании вначале таблицы.

Заметим, что решение задачи интерполяции по Ньютону имеет некоторые преимущества по сравнению с решением задачи интерполяции по Лагранжу. Каждое слагаемое интерполяционного многочлена Лагранжа зависит от всех значений табличной функции y_i , i=0,1,…n. Поэтому при изменении количества узловых точек N и степени многочлена n (n=N-1) интерполяционный многочлен Лагранжа требуется строить заново. В многочлене Ньютона при изменении количества узловых точек N и степени многочлена n требуется только добавить или отбросить соответствующее число стандартных слагаемых в формуле Ньютона (2). Это удобно на практике и ускоряет процесс вычислений.

Программирование функции формулы Ньютона

Для построения многочлена Ньютона по формуле (1) организуем циклический вычислительный процесс по . При этом на каждом шаге поиска находим разделенные разности k-го порядка. Будем помещать разделенные разности на каждом шаге в массив Y.

Тогда рекуррентная формула (3) будет иметь вид:

(4)

В формуле Ньютона (2) используются разделенные разности -го порядка, подсчитанные только для участков т.е. разделенные разности -го порядка для . Обозначим эти разделенные разности k-го порядка как . А разделенные разности, подсчитанные для , используются для расчетов разделенных разностей более высоких порядков.

Используя (4), свернем формулу (2). В результате получим

(5)

где

– значение табличной функции (1) для .

– разделенная разность -го порядка для участка .