Курсовая работа: Интерполяция функции одной переменной методом Ньютона

Для вычисления Р удобно использовать рекуррентную формулу внутри цикла по .

Схема алгоритма интерполяции по Ньютону представлена на рисунке:

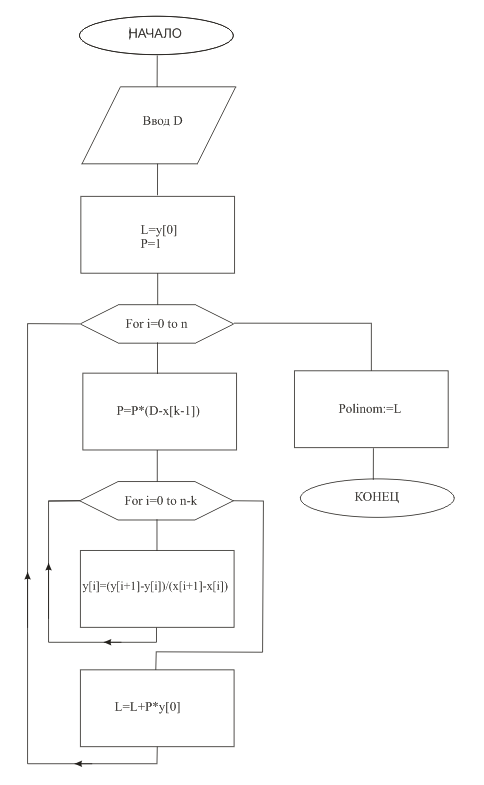
Function POlinom(n: integer; d:real; x,y :per):real;

var

l:real;

k,i:integer;

p: real;

begin

L:=y[0];

P:=1;

for k:=1 to n do begin

P:=P*(D-X[k-1]);

for i:=0 to (n-k) do begin

Y[i]:=(y[i+1]-y[i])/(x[i+k]-x[i]);

end;

L:=L+P*y[0];

end;

Polinom:=l;

end;

где

n – количество узлов

x[i],y[i] – табличные значения функции

D – точка, в которой необходимо вычислить значение l

Обзор литературных источников

1. Численные методы

Численные методы являются одним из мощных математических средств решения задачи. Простейшие численные методы мы используем всюду, например» извлекая квадратный корень на листке бумаги. Есть задачи, где без достаточно сложных численных методов не удалось бы получить ответа; классический пример—открытие Нептуна по аномалиям движения Урана.

В современной физике таких задач много- Более того, часто требуется выполнить огромное число действий за короткое время, иначе ответ будет не нужен. Например, суточный прогноз погоды должен быть вычислен за несколько часов; коррекцию траектории ракеты надо рассчитать за несколько минут (напомним, что для расчета орбиты Нептуна Леверье потребовалось полгода); режим работы прокатного стана должен исправляться за секунды. Это немыслимо без мощных ЭВМ, выполняющих тысячи или даже миллионы операций в секунду.

Современные численные методы и мощные ЭВМ дали возможность решать такие задачи, о которых полвека назад могли только мечтать. Но применять численные методы далеко не просто. Цифровые ЭВМ умеют выполнять только арифметические действия и логические операции. Поэтому помимо разработки математической модели, требуется еще разработка алгоритма, сводящего все вычисления к последовательности арифметических и логических действий. Выбирать модель и алгоритм надо с учетом скорости и объема памяти ЭВМ: чересчур сложная модель может оказаться машине не под силу, а слишком простая — не даст физической точности.