Курсовая работа: Использование метода ветвей и границ при адаптации рабочей нагрузки к параметрам вычислительного процесса
откуда искомая вероятность
![]() (1)
(1)
Если эта формула известна, то можно осуществить физический эксперимент, произведя несколько партий выстрелов (по десять в каждой) по реальной мишени. Но проще выполнить математический эксперимент на вычислительной машине следующим образом. Датчик случайных чисел выдаст в цифровом виде значение случайной величины ξ, подчиняющейся равномерному закону распределения в интервале [0,1]. Вероятность неравенства ξ<p равна p, т.е.
P {ξ<p}=p.
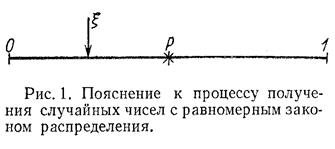
Для пояснения целесообразно обратиться к рис. 1, на котором весь набор случайных чисел представляется в виде точек отрезка [0,1]. Вероятность попадания случайной величины ξ, имеющей равномерное распределение в интервале [0,1], в интервал [0, p] (где ![]() ) равна длине этого отрезка, т.е. p. Поэтому на каждом такте моделирования полученное число ξ сравнивают с заданной вероятностью p. Если ξ<p, то регистрируется попадание в мишень, в противном случае – промах. Далее проводят серию из десяти тактов и подсчитывают чётное или нечётное число попаданий. При большом числе серий (100–1000) получается вероятность, близкая к той, которая определяется по формуле (1).
) равна длине этого отрезка, т.е. p. Поэтому на каждом такте моделирования полученное число ξ сравнивают с заданной вероятностью p. Если ξ<p, то регистрируется попадание в мишень, в противном случае – промах. Далее проводят серию из десяти тактов и подсчитывают чётное или нечётное число попаданий. При большом числе серий (100–1000) получается вероятность, близкая к той, которая определяется по формуле (1).
Различают две области применения метода Монте-Карло. Во-первых, для исследования на вычислительных машинах таких случайных явлений и процессов, как прохождение элементарных ядерных частиц (нейтронов, протонов и пр.) через вещество, системы массового обслуживания (телефонная сеть, система парикмахерских, система ПВО и пр.), надёжность сложных систем, в которых выход из строя элементов и устранения неисправностей являются случайными процессами, статистическое распознавание образов. Это – применение статистического моделирования к изучению так называемых вероятностных систем управления.
Этот метод широко применяется и для исследования дискретных систем управления, когда используются кибернетические модели в виде вероятностного графа (например, сетевое планирование с β-распределением времени выполнением работ) или вероятностного автомата.
Если динамика системы управления описывается дифференциальными или разностными уравнениями (случай детерминированных систем управления) и на систему, например угловую следящую систему радиолокационной станции воздействуют случайные сигналы, то статическое моделирование также позволяет получить необходимые точностные характеристики. В данном случае с успехом применяются как аналоговые, так и цифровые вычислительные машины. Однако, учитывая более широкое применение при статистическом моделировании цифровых машин, рассмотрим в данном разделе вопросы, связанные только с этим типом машин.
Вторая область применения метода Монте-Карло охватывает чисто детерминированные, закономерные задачи, например нахождение значений определённых одномерных и многомерных интегралов. Особенно проявляется преимущество этого метода по сравнению с другими численными методами в случае кратных интегралов.
При решении алгебраических уравнений методом Монте-Карло число операций пропорционально числу уравнений, а при их решении детерминированными численными методами это число пропорционально кубу числа уравнений. Такое же приблизительно преимущество сохраняется вообще при выполнении различных вычислений с матрицами и особенно в операции обращения матрицы. Надо заметить, что универсальные вычислительные машины не приспособлены для матричных вычислений и метод Монте-Карло, применённый на этих машинах, лишь несколько улучшает процесс решения, но особенно преимущества вероятностного счёта проявляются при использовании специализированных вероятностных машин. Основной идеей, которая используется при решении детерминированных задач методом Монте-Карло, является замена детерминированной задачи эквивалентной статистической задачей, к которой можно применять этот метод. Естественно, что при такой замене вместо точного решения задачи получается приближённое решение, погрешность которого уменьшается с увеличением числа испытаний.
Эта идея используется в задачах дискретной оптимизации, которые возникают при управлении. Часто эти задачи сводятся к перебору большого числа вариантов, исчисляемого комбинаторными числами вида N=![]() . Так, задача распределения n видов ресурсов между отраслями для n>3 не может быть точно решена на существующих цифровых вычислительных машинах (ЦВМ) и ЦВМ ближайшего будущего из-за большого объёма перебора вариантов. Однако таких задач возникает очень много в кибернетике, например синтез конечных автоматов. Если искусственно ввести вероятностную модель-аналог, то задача существенно упростится, правда, решение будет приближённым, но его можно получить с помощью современных вычислительных машин за приемлемое время счёта.
. Так, задача распределения n видов ресурсов между отраслями для n>3 не может быть точно решена на существующих цифровых вычислительных машинах (ЦВМ) и ЦВМ ближайшего будущего из-за большого объёма перебора вариантов. Однако таких задач возникает очень много в кибернетике, например синтез конечных автоматов. Если искусственно ввести вероятностную модель-аналог, то задача существенно упростится, правда, решение будет приближённым, но его можно получить с помощью современных вычислительных машин за приемлемое время счёта.
При обработке больших массивов информации и управлении сверхбольшими системами, которые насчитывают свыше 100 тыс. компонентов (например, видов работ, промышленных изделий и пр.), встаёт задача укрупнения или эталонизации, т.е. сведения сверхбольшого массива к 100–1000 раз меньшему массиву эталонов. Это можно выполнить с помощью вероятностной модели. Считается, что каждый эталон может реализоваться или материализоваться в виде конкретного представителя случайным образом с законом вероятности, определяемым относительной частотой появления этого представителя. Вместо исходной детерминированной системы вводится эквивалентная вероятностная модель, которая легче поддаётся расчёту. Можно построить несколько уровней, строя эталоны эталонов. Во всех этих вероятностных моделях с успехом применяется метод Монте-Карло. Очевидно, что успех и точность статистического моделирования зависит в основном от качества последовательности случайных чисел и выбора оптимального алгоритма моделирования.
Задача получения случайных чисел обычно разбивается на две. Вначале получают последовательность случайных чисел, имеющих равномерное распределение в интервале [0,1]. Затем из неё получают последовательность случайных чисел, имеющих произвольный закон распределения. Один из способов такого преобразования состоит в использовании нелинейных преобразований. Пусть имеется случайная величина X, функция распределения вероятности для которой
![]() .
.
Если y является функцией x, т.е. y=F(x), то ![]() и поэтому
и поэтому ![]() . Таким образом, для получения последовательности случайных чисел, имеющих заданную функцию распределения F(x), необходимо каждое число y с выхода датчика случайных чисел, который формирует числа с равномерным законом распределения в интервале [0,1], подать на нелинейное устройство (аналоговое или цифровое), в котором реализуется функция, обратная F(x), т.е.
. Таким образом, для получения последовательности случайных чисел, имеющих заданную функцию распределения F(x), необходимо каждое число y с выхода датчика случайных чисел, который формирует числа с равномерным законом распределения в интервале [0,1], подать на нелинейное устройство (аналоговое или цифровое), в котором реализуется функция, обратная F(x), т.е.
![]() . (2)
. (2)
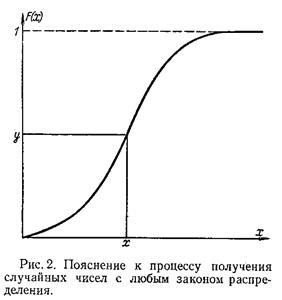
Полученная таким способом случайная величина X будет иметь функцию распределения F(x). Рассмотренная выше процедура может быть использована для графического способа получения случайных чисел, имеющих заданный закон распределения. Для этого на миллиметровой бумаге строится функция F(x) и вводится в рассмотрение другая случайная величина Y, которая связана со случайной величиной X соотношением (2) (рис. 2).
Так как любая функция распределения монотонно неубывающая, то
![]() .
.
Отсюда следует, что величина Y имеет равномерный закон распределения в интервале [0,1], т. к. её функция распределения равна самой величине
![]() .
.
Плотность распределения вероятности для Y
![]() .
.
Для получения значения X берётся число из таблиц случайных чисел, имеющих равномерное распределение, которое откладывается на оси ординат (рис. 2), и на оси абсцисс считывается соответствующее число X. Повторив неоднократно эту процедуру, получим набор случайных чисел, имеющих закон распределения F(x). Таким образом, основная проблема заключается в получении равномерно распределённых в интервале [0,1] случайных чисел. Один из методов, который используется при физическом способе получения случайных чисел для ЭВМ, состоит в формировании дискретной случайной величины, которая может принимать только два значения: 0 или 1 с вероятностями
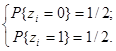
Далее будем рассматривать бесконечную последовательность z1 , z2 , z3 ,… как значения разрядов двоичного числа ξ* вида
![]()