Курсовая работа: Исследование движения механической системы с двумя степенями свободы

Свяжем подвижную систему отсчета с движущимся вдоль канала шариком. Ось проведём вдоль канала, причём возрастание координаты сонаправленно с движением шарика относительно трубки; а ось направим перпендикулярно ей. Вращение треугольника вместе с системой координат вокруг шарнира является переносным движением для шарика. Относительным движением является его перемещение вдоль канала .

Дифференциальное уравнение движения (2.1) для данной системы примет вид:

(2.2)

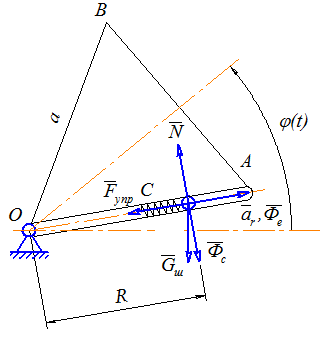
Рисунок 2.1. Исследование относительного движения материальной точки

Абсолютные значения сил:

;

, где ;

– при постоянной угловой скорости вращения , тогда , где – радиус вращения шарика вокруг шарнира ;

, т. к. угол между относительной и угловой скоростями прямой, отсюда , а направление определяется по правилу Жуковского.

Возьмём проекцию дифференциального уравнения относительного движения (2.2) на координатную ось подвижной системы координат:

(2.3)

Радиус переносного вращения шарика:

(2.4)

С учётом значений сил и формулы (2.4), уравнение (2.3) принимает вид:

Отсюда получаем значение реакции связи :

(2.5)

В приложении к курсовой работе изображён график зависимости (рис. 2).

Теперь спроецируем дифференциальное уравнение (2.2) на координатную ось :

(2.6)

При подстановке известных значений получим:

(2.7)

Приведём (2.7) к следующему виду:

(2.8)

Здесь – это собственная частота. Для нахождения зависимости решим данное уравнение.

– решение искомого дифференциального уравнения будет складываться из общего решения соответствующего однородного уравнения и любого частного решения .

Общее решение имеете вид: (2.9).

Найдём частное решение уравнения (2.8), оно будет иметь вид: . Первая и вторая производные: , .