Курсовая работа: Исследование движения механической системы с двумя степенями свободы

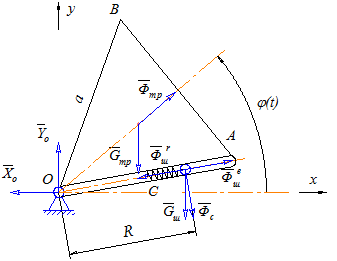
Рисунок 3.1.1. Составление уравнения движения твердого тела с помощью теоремы об изменении кинетического момента

, где модуль переносной скорости равен .

(3.1.4)

, – момент инерции треугольника относительно шарнира . Определим его по теореме Штейнера:

(3.1.5)

(3.1.6)

Учитывая (3.1.4) и (3.1.6), кинетический момент системы равен:

(3.1.7)

Продифференцируем выражение (3.1.7):

(3.1.8)

Подставив найденные значения в (3.1.2), теорема об изменении кинетического момента примет вид:

(3.1.9)

3.2 Определение закона изменения внешнего момента, обеспечивающего постоянство угловой скорости

При действии внешнего момента , обеспечивающего равномерное вращение механической системы вокруг шарнира , последнее слагаемое в левой части равенства (3.1.9) обращается в нуль:

, ; отсюда .

Тогда выражение (3.1.9) примет вид:

(3.2.1)

направлен противоположно главному моменту внешних сил, то есть, против часовой стрелки.

Внешний момент, обеспечивающий равномерное вращение конструкции, равен:

(3.2.2)

В приложении к курсовой работе изображён график зависимости (рис. 3).

4. Определение реакций в опорах вращающегося тела

Определим реакции в опоре вращающегося тела методом кинетостатики. Он заключается в решении задачи динамики средствами (уравнениями) статики. Для каждой точки механической системы справедливо основное уравнение динамики:

(4.1)

Здесь и – масса и ускорение некоторой точки системы; – сумма всех активных сил и реакций связей, приложенных к ней.

Основному уравнению динамики (4.1) можно придать вид уравнения статики:

(4.2)

Здесь – сила инерции точки механической системы.