Курсовая работа: Исследование движения механической системы с двумя степенями свободы

Для заданной механической системы уравнение статики (4.2) имеет вид:

(4.3)

Для определения реакции шарнира нам необходимо и достаточно взять за координатные оси – неподвижные оси и , и определить составляющие реакции шарнира на эти оси:

(4.4)

Отсюда:

Подставив значения сил, получим:

(4.5)

Теперь спроецируем (4.2) на неподвижную ось :

(4.6)

Отсюда:

Подставив известные значения сил, получим:

(4.7)

Полную реакцию в шарнире можно найти по формуле: , где и определяются выражениями (4.5) и (4.7); график её зависимости от времени приведён в приложении к курсовой работе (рис. 4).

5. Исследование движения механической системы с двумя степенями свободы с помощью уравнений Лагранжа II рода

5.1 Составление уравнений движения системы методом Лагранжа

Уравнения второго рода являются одним из наиболее удобных приёмов составления уравнений движения механических систем. Они имеют следующий вид:

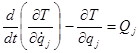
(5.1.1)

Здесь – кинетическая энергия системы; , , , – обобщённые координаты, скорости и силы соответственно; – число степеней свободы.

Уравнения (5.1.1) образуют систему уравнений второго порядка относительно функций , а порядок данной системы равен . Форма уравнений Лагранжа не зависит от выбора обобщённых координат . В связи с этим говорят, что уравнения Лагранжа второго рода обладают свойством инвариантности.

Как видно из (5.1.1), для получения уравнений Лагранжа необходимо найти соответствующие производные от кинетической энергии системы и определить обобщённые силы.

Определим кинетическую энергию системы. Она будет складываться из кинетических энергий треугольника и шарика: .

Подставив значение из (3.1.5), получим:

(5.1.2)

Кинетическая энергия шарика определяется его массой и относительной и переносной скоростями: