Курсовая работа: Исследование метода дифференцирования по параметру для решения нелинейных САУ
Xm +1 = Xm + ( hm /2)·( K 1 + K 2 ), где
K 1 = F ( Xm , tm ), K 2 = F ( Xm + hm · K 1 , tm + hm ).
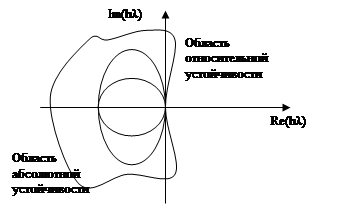
Ошибка аппроксимации εα = kh 3 т . Область абсолютной устойчивости показана на рис. 1.3 (кривая 2). Область относительной устойчивости - вся правая полуплоскость.
Алгоритм метода Рунге-Кутта 4-го порядка:
Xm +1 = Xm + ( hm /6) · ( K 1 + 2 K 2 + 2 K 3 + K 4 ), где
K 1 = F ( Xm , tm ), K 2 = F ( Xm + ( hm /2)· K 1 , tm + hm /2);
K3 = F(Xm + (hm /2) ·K2 , tm + hm /2);
K4 = F(Xm + h·K3 , tm + hm );
Ошибка аппроксимации εα =kh 5 т . Область абсолютной устойчивости показана на рис. 1.3 (кривая 3). Область относительной устойчивости - вся правая полуплоскость.
 |
![]() 1
1
 2
2
![]() 3
3
Рис. 1.3
1.4 Метод Ньютона
Итерационная формула дискретного метода Ньютона имеет вид
Xm +1 = Xm – J -1 ( Xm ) · F ( Xm ) ,
где J (Х m ) = F / X / X = Xm – матрица Якоби.
Характеристики метода.
1. Сходимость.
Условие сходимости метода
ρ( G ’Х (Х))= ρ( I – ( J -1 (Х) · F (Х))/ Х )<1.
Имеем ρ( I – J -1 (Х*) · F / Х (Х*))=0 ; это означает, что метод обладает локальной сходимостью, т.е. сходится только вблизи точного решения. Поэтому при реализации метода дифференцирования по параметру вначале нужно получить приближенное значение. Чем ближе к Х* , тем быстрее сходится метод.
2. Выбор начального приближения Х0 .
Поскольку метод сходится только вблизи точного решения, значит, начальное приближение также нужно выбирать вблизи Х*. Насколько близко, зависит от скорости изменения функции F (Х) вблизи Х* : чем выше скорость, тем меньше область, где соблюдается условие сходимости.
3. Скорость сходимости.
Она определяется соотношением
|| Em +1 ||= Cm || Em ||1+ Р ,
0<р<1 . При Х→Х* величина р→1 . Это значит, что вблизи точного решения скорость сходимости близка к квадратичной.
4. Критерий окончания итераций.
Таким критерием может быть любое соотношение из описанных выше в обобщенном алгоритме решения нелинейных САУ.
1.5 Дискретный метод Ньютона