Министерство Образования РФ

НГТУ

Кафедра экономической информатики

Курсовая работа по курсу

«Численные методы в экономике»:

Исследование неявного метода Эйлера для линейной системы

ОДУ с постоянным и переменным шагом

Введение

Целью данного проекта является исследование неявного метода Эйлера для решения линейных систем ОДУ с постоянным и переменным шагом. В ходе работы будет создана программа на языке матрично-ориентированной системы MatLAB и приведена математическая интерпретация метода. Также будет представлено влияние величины шага интегрирования и начальных значений на качество и точность вычислений. Будут проанализированы результаты и сделаны выводы.

1. Постановка задачи. Математическое описание метода

Для линейных систем

( Х = АХ+В U ( t ) )

эта проблема решается очень просто. Нелинейные системы приходится линеаризовать в точке X^m , t_m , затем уже решать приведенным ниже способом:

Все значения в этой формуле, кроме X^{m +1} , которое нужно найти, известны (I – единичная матрица). Это получается линейная система, которая решается стандартными методами.

Неявный метод Эйлера: Группа неявных методов Рунге-Кутта используется для интегрирования "жестких" систем. Неявный метод Эйлера (Рунге-Кутта 1-го порядка) описывается с помощью следующей формулы:

X^{m +1} = X^m + h_m F ( X^{m +1} , t_{m +1} )

Как уже говорилось ранее, чтобы определить X^{m +1} надо решить данную систему. При известных значениях величин X^m , h_m , t_{m +1} - это система нелинейных уравнений относительно X^{m +1} . Ее необходимо решать на каждом шаге по времени m.

Для линейных систем

( Х = АХ+В U ( t ) )

эта проблема решается очень просто. Нелинейные системы приходится линеаризовать в точке X^m , t_m , затем уже решать приведенным ниже способом:

Все значения в этой формуле, кроме X^{m +1} , которое нужно найти, известны (I – единичная матрица). Это получается линейная система, которая решается стандартными методами.

Рассмотрим характеристики метода.

1.Точность. Ошибка аппроксимации по величине равна ошибке аппроксимации явного метода Эйлера, но она противоположна по знаку:

 _i ^am = -0.5h² _m X^.. (t^- )

где h_m <= t^- <= t_{m +1}

2. Устойчивость метода

Сделав линеаризацию функции F(X,t)в точке X^m , h_m , t_{m +} 1 получим уравнение относительно y^{m +1}

Y^m+1 = y^m +h  y^m+1

Характеристического уравнение r-hlr-1=0 "дает" корень r=1/(1-hl).

1. Условие абсолютной устойчивости (Re(hl)<0): |1/(1-hl)|<1 или по другому

|1-hl|>1. Последнее неравенство можно преобразовать к виду:

[1-Re(h  )]² + Im((h  )]² >1

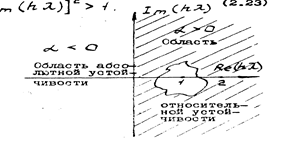
С учетом того, что мы рассматриваем ситуацию, когда Re(hl)<0, область абсолютной устойчивости, как следует из неравенства [1- Re ( h )]² + Im (( h )]² >1 - вся левая полуплоскость.

2. Условия относительной устойчивости

(Re(hl)>0): |1/(1-hl)|>1.

С учетом ограничения на скорость изменения приближенного решения относительного точного:

|1/(1- h l )|<| e^{h l} |

Из этого соотношения следует, что при |hl|®1 левая часть стремится к бесконечности. Это значит, что в правой полуплоскости имеется некоторая область, где неравенство

|1/(1- h l )|<| e^{h l} | не выполняется.

3. Выбор шага

4. Условия выбора шага диктуются требованиями абсолютной или относительной устойчивости. Однако область абсолютной устойчивости – вся левая полуплоскость. Поэтому шаг с этой точки зрения может быть любым.

Условия устойчивости жестче, так как есть область, где они могут быть нарушены. Можно показать, что эти условия будут выполнены, если в процессе решения задачи контролировать e^{a m} _i , а шаг корректировать. Таким образом, шаг можно выбирать только из условий точности, при этом условия устойчивости будут соблюдены автоматически. Сначала задается допустимая погрешность аппроксимации:

e ^{a gon} _i <=0.001| X_i | _max, i=1,n

Процедура выбора шага в процессе численного интегрирования состоит в следующем:

1. Решая систему

X^{m +1} = X^m + h_m F ( X^{m +1} , t_{m +1}

--> ЧИТАТЬ ПОЛНОСТЬЮ <--