Курсовая работа: Исследование неявного метода Эйлера для линейной системы ОДУ с постоянным и переменным шагом

получаем очередную точку решения системы

X^o =F(X,t).

2. Оцениваем величину ошибки аппроксимации по формуле:

e ^{a m} _i = |h_m /(h_m +h_m+1 )[(X_i ^m+1 – X_i ^m ) – h_m /h_m-1 (X^m _i – X^m-1 _i ]|

3. Действительное значение ошибки аппроксимации сравнивается с допустимым

e ^{a m} _i < e ^{a gon} _i , i=1,n..

4. Если хотя бы для одного i неравенство не соблюдается, то шаг h_m уменьшается, в противном случае – увеличивается по сравнению с ранее принятым. Вопрос состоит в том как это сделать. Самый простой вариант – уменьшить в два раза. Вычисления повторяются с п.1.

5. Если упомянутые выше неравенства выполняются для всех i, то рассчитывается следующий шаг:

h_i ^m+1 =  ( e ^{a gon} _i / | e ^{a m} _i |)*h^m , i=1,n

6. Шаг выбирается одинаковым для всех элементов вектора Х:

h_{m +1} = min h^{m +1} _{i .}

6. Вычисляется новый момент времени

7. t_{m +2} = t_{m +1} + h_{m +1} и алгоритм повторяется с п.1.

Интегрирование «жесткой» системы ОДУ: «Жесткими» называются системы, число обусловленности которых:

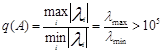
В решении системы присутствуют экспоненты, сильно отличающиеся друг от друга по скорости затухания. После затухания быстрой экспоненты наступает медленная часть решения, казалось бы шаг интегрирования можно увеличить. Однако требования устойчивости должны выполняться на всем участке решения. Это требует больших затрат машинного времени. Таким образом, ограниченность области абсолютной устойчивости делает явный метод Рунге-Кутта 4-го порядка непригодным для интегрирования «жестких» линейных систем ОДУ.

4. Описание программного обеспечения

Общие сведения и требования к ПО : Программа состоит из 3-х файлов, написанных на языке MatLAB - rkpost1.m (для метода с постоянным шагом), rkper1.m(для метода с переменным шагом) и тестовая программа для них (test.m).

Функциональное назначение: Программа предназначена для решения линейных систем ОДУ в среде MatLABметодом численного интегрирования Эйлера (Рунге-Кутта 1-го порядка).

Программа:

- rkper1.m

function [tout, yout, eout]=rkper1(funA, funB, funU, t0, tfinal, y0, ep, trace)

if nargin<7, ep=0.001; end

if nargin<8, trace=1; end

t=t0; y=y0;

tout=t; yout=y.';

h1=(tfinal-t)/20000;

h=h1*200;

if trace

clc, t, h, y

end

A=feval(funA);

B=feval(funB);

n=ones(max(size(y0)),1);

I=diag(n,0);

ym1=y0; yp1=y0;