6. Анализ результатов. Выводы

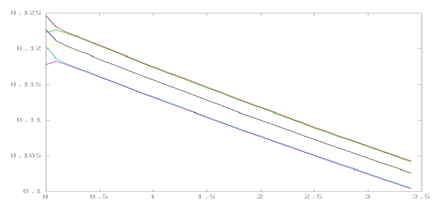
Ниже показаны полученные графики функций и ошибок:

График1:

Var, XX0=[0.1;0.1] X0=[0.5;0.5] X0=[1;1]

График2 :

Var, EX0=[0.1;0.1] X0=[0.5;0.5] X0=[1;1]

График 3:

Const, X h=0.1, X0=[0.2;0.2] h=0.01, X0=[0.2;0.2] h=0.005, X0=[0.2;0.2]

График4 :

Const, E h=0.1, X0=[0.2;0.2] h=0.01, X0=[0.2;0.2] h=0.005, X0=[0.2;0.2]

График 5 :

Const, X h=0.1, X0=[0.1;0.1] h=0.1, X0=[0.5;0.5] h=0.1, X0=[1;1]

График6:

Const, E h=0.1, X0=[0.1;0.1] h=0.1, X0=[0.5;0.5] h=0.1, X0=[1;1]

Пояснения :

Var – метод с переменным шагом;

Const – метод с постоянным шагом.

X0=[0.1;0.1], X0=[0.5;0.5], X0=[1;1] отражают цветовую гамму на графике.

X – графики функций;

E – графики ошибок.

h – шаг, X 0 – начальное значение X.

Рисунки с 7 -12 аналогичны рисункам 1-6 (соответственно) по начальным данным и отличаются лишь жесткостью решаемой системы.

Выводы

Видим, что при увеличении начального значения происходит лишь параллельный сдвиг решения, однако график ошибки перемещается в противоположную сторону (при увеличении начального значения она уменьшается и наоборот), причем непропорционально. Следовательно, при увеличении начального значения X ошибка уменьшается, однако с увеличением t это изменение становится все менее и менее заметным. Это характерно как для метода с переменным шагом, так и для метода с постоянным шагом. Кроме того, для метода с постоянным шагом увеличение шага приводит к уменьшению точности решения. Что касается жесткой системы, то для нее характерно прямолинейное конечное решение. С уменьшением шага ошибка, посчитанная по методу Рунге, уменьшается. При увеличении начального X происходит параллельный сдвиг графика конечного решения. Если в случае нежесткой системы графики решений разных составляющих X находятся далеко друг от друга, то при решении жесткой системы получаются очень близкие графики.

Заключение

В ходе выполнения работы был изучен неявный метод Эйлера для решения линейных систем ОДУ. В ходе реализации проекта и проведения тестирования была проверена справедливость теоретических выкладок. Получены сведения о зависимости точности интегрирования от величины и способа выбора шага, а также от начальных значений переменных.

Используемая литература

1. Сарычева О.М. Численные методы. – Новосибирск, 1995г. – 65с.

2. Бахвалов Н.С. Численные методы. Ч1.- М: Наука, 1975г. – 632с., илл.

3. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах . – М: Наука, 1972г. - 368с