Курсовая работа: Кінематичний аналіз плоских важільних, кулачкових і зубчастих механізмів

Відповідно до першого рівняння через крапку із плану швидкостей проводимо пряму, перпендикулярну до DС, а для рішення другого рівняння необхідно через полюс p провести пряму, паралельну напрямної X–X. На перетинанні цих прямих і буде перебувати шукана крапка d.

Величини швидкостей визначимо, множачи довжини векторів на плані швидкостей на масштабний коефіцієнт

Швидкість центра мас S₄ ланки 4 визначимо по теоремі подоби

,

звідки

Отже,

У зазначеній послідовності виробляється побудова планів швидкостей для всіх 12-ти положень механізму. Причому, вектори, що виходять із полюса P, зображують абсолютні швидкості, а відрізки з'єднуючі кінці цих векторів – відносні швидкості крапок.

Обчислені в такий спосіб величини швидкостей зводимо в таблицю 2.1.

Визначимо кутові швидкості ланок

Напрямок кутової швидкості ланки AВ визначиться, якщо перенести вектор швидкості крапки B на схемі механізму й установити напрямок обертання ланки AB щодо крапки А під дією цього вектора. У розглянутому випадку в положенні 1 механізму кутова швидкість спрямована проти годинникової стрілки.

Напрямок кутової швидкості шатуна 4 визначає вектор , якщо його перенести із плану швидкостей у крапку D на схемі механізму. У положенні 1 кутова швидкість спрямована проти годинникової стрілки.

Таблиця 2.1

№	VО	VА	VB	VS 2	VС	VD	VS 4	VВА	VDС	ω1	ω2	ω4
	м/з									с-1
0	0	20,8	0	14	20,8	20,8	20,8	20,8	0	188,4	60,03	0
1	0	20,8	13,4	16,6	20,8	21,2	20,4	18	10,8	188,4	51,95	31,17
2	0	20,8	21,2	20,4	20,8	13,4	16,6	10,8	18	188,4	31,17	51,95
3	0	20,8	20,8	20,8	20,8	0	0	0	20,8	188,4	0	60,03
4	0	20,8	15	18,2	20,8	13,4	16,6	10,8	18	188,4	31,17	51,95
5	0	20,8	7,6	15,6	20,8	21,2	20,4	18	10,8	188,4	51,95	31,17
6	0	20,8	0	14	20,8	20,8	20,8	20,8	0	188,4	60,03	0
7	0	20,8	7,6	15,6	20,8	15	18,4	18	10,8	188,4	51,95	31,17
8	0	20,8	15	18,2	20,8	7,6	14,8	10,8	18	188,4	31,17	51,95
9	0	20,8	20,8	20,8	20,8	0	0	0	20,8	188,4	0	60,03
10	0	20,8	21,2	20,4	20,8	7,6	14,8	10,8	18	188,4	31,17	51,95
11	0	20,8	13,4	16,6	20,8	15	18,4	18	10,8	188,4	51,95	31,17

2.3 Побудова планів прискорень

Послідовність побудови плану прискорень також визначається формулою будови механізму. Спочатку визначимо прискорення провідної крапки A. При початкової ланки ОА крапка А має тільки нормальне прискорення:

Прискорення крапки А а_А на плані прискорень зобразимо вектором , що спрямований по ланці ОА від крапки А к крапці О. Масштабний коефіцієнт плану прискорень вибираємо стандартним.

Вектор і є план прискорень початкової ланки ОА (кривошипа).

А тепер побудуємо план прискорень групи 2, 3. Тут відомі прискорення крапок А и В. Запишемо два векторних рівняння, розглядаючи рух крапки B відносно А и стосовно крапки B₀ :

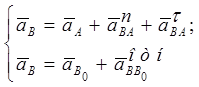
де - нормальне прискорення у відносному русі крапки B стосовно крапки А;

- тангенціальне прискорення в тім же русі;

- прискорення крапки B₀ напрямної X–X;

- прискорення крапки B повзуну щодо крапки B₀ приналежний.