Курсовая работа: Колебания кристаллической решетки

Первое слагаемое в правой части – сила, действующая на n -й атом со стороны n +1-го атома, второе – сила, действующая со стороны n –1-го атома.

После упрощения получим:

(2).

Система таких уравнений, записанных для каждого атома, полностью описывает колебания цепочки.

Если рассматривать только длинноволновые колебания, т. е. колебания с длиной волны много большей периода цепочки a , то можно заменить разность u_{n +1} –u_n на (∂ u_n /∂ x )a , а величину, стоящую в правой части (2) – на γ a ² (∂² u /∂ x ² ). В результате получим волновое уравнение:

(3).

Решением которого являются волны u = A exp(ikx –iω t ) с линейным законом дисперсии ω = |k | (звуковые волны). Здесь - скорость звука: . Но мы решим задачу точно и рассмотрим колебания со всеми возможными длинами волн.

Будем искать колебания, зависящие от времени по гармоническому закону: u_n = C_n e ^{–iω t} (5).

Здесь ω – частота колебаний, одна и та же для всех атомов (такие колебания называются гармоническими). C_n – комплексная амплитуда колебаний n -го атома. Напомним, что колебания описывает вещественная часть уравнения (5), но технически удобно пользоваться комплексным решением.

Такая подстановка – стандартный метод решения линейных систем уравнений с постоянными коэффициентами. В силу линейности уравнений, колебание с произвольной временной зависимостью может быть разложено в интеграл (ряд) Фурье по гармоническим колебаниям.

Изуравнения (2) для амплитуды C_n получаем уравнение:

(6).

Эти уравнения образуют бесконечную систему линейных уравнений. Если применить к цепочке граничные условия Борна-Кармана, то система будет конечной. (Заметим, что условия Борна-Кармана в одномерном случае эквивалентны тому, что цепочка достаточно большой длины L замкнута в кольцо). Тогда, приравняв определитель нулю, можно найти частоты колебаний, а затем, решив систему уравнений для каждой из найденных частот – соответствующие амплитуды.

Но мы поступим иначе. Будем искать решение в виде плоской волны:

(7).

Подставив это выражение в (6), получим:

(8)

Разделим последнее уравнение на exp(ikx_n ) и воспользуемся тем, что x_{n +1} = x_n +a , x_{n –1} = x_n –a : –M ω ² = γ (e^ika +e ^{– ika} –2) (9).

Таким образом, подстановка в виде плоской волны оказалась верной: мы избавились от номера атома n и получили уравнение, связывающее ω и k , то есть уравнение, определяющее закон дисперсии волн.

Поскольку: (10), то (11).

Мы получаем закон дисперсии для упругих колебаний одномерной цепочки: (12).

Итак, мы пришли к выводу, что смещения атомов при колебании одномерной цепочки описываются плоской гармонической волной:

(13).

Точнее, колебания представляют собой произвольную сумму таких волн. Здесь φ – фаза комплексной амплитуды A : A = |A |exp(iφ ). Смещение – вещественная величина, которая описывается вещественной частью комплексной плоской гармонической волны, что явно записано в (13). В дальнейшем, при описании вещественных колебаний комплексной плоской волной, будем для краткости опускать обозначение вещественной части.

Волновой вектор k в плоской волне (13) может, вообще говоря, быть любым. Но вследствие дискретности цепочки (x_n может принимать лишь дискретный набор значений na ) плоские волны, волновые вектора которых отличаются друг от друга на произвольный вектор обратной решетки 2π l /a , описывают одно и то же колебание. (Здесь l — любое целое число).

Действительно, так как x_n = na , т:

(14).

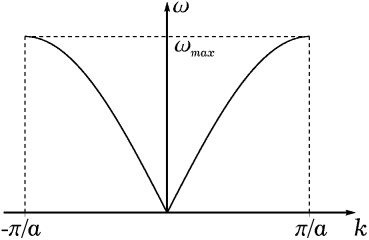
Поэтому достаточно рассматривать волновые вектора, лежащие в первой зоне Бриллюэна –π /a <k <π /a . Крайние значения волнового вектора ±π /a соответствуют одному и тому же колебанию с минимальной длиной волны λ = 2π /k = 2a . При такой длине волны соседние атомы цепочки движутся в противофазе. Интуитивно ясно, что короче длина волны быть уже не может.

График зависимости ω (k ) для одномерной цепочки с одним атомом в примитивной ячейке изображен на рис. 1.2.

« 1 2 3 4 5 6 7 » К-во Просмотров: 420 Бесплатно скачать Курсовая работа: Колебания кристаллической решетки >>> Скачать <<< Меню Поиск