Курсовая работа: Колебания кристаллической решетки

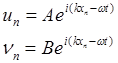(23).

Амплитуды колебаний маленького и большого атомов A и B в общем случае разные как по абсолютной величине, так и по фазе.

После подстановки (23) в (22) получим линейную однородную систему уравнений для A и B :

–M ₁ ω ² A = γ (Be^ika +B –2A )

–M ₂ ω ² B = γ (A +Ae ^–ika –2B ) (24).

Перепишем ее в стандартном виде:

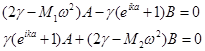(25)

Такая система имеет решения лишь в том случае, когда ее определитель равен нулю. Приравнивая нулю определитель (25) получим уравнение, связывающее ω и k , т. е. дисперсионное уравнение:

M ₁ M ₂ ω ⁴ – 2γ (M ₁ +M ₂ )ω ² +2γ ² (1–cos ka ) = 0 (26).

Это уравнение удобно переписать, использую приведенную массу атомов примитивной ячейки μ :

(27).

(28)

Его решения имеют вид:

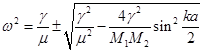(29)

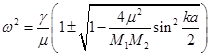или (30).

Величина 4μ ² /(M ₁ M ₂ ) при любых M ₁ , M ₂ не превосходит единицы, поэтому подкоренное выражение всегда неотрицательно.

1.3. Трехмерный кристалл

Мы рассмотрели колебания в одномерной цепочке. Подобным образом могут быть описаны и колебания решетки трехмерного кристалла.

Предположим, что примитивная ячейка кристалла состоит из l атомов. Каждый атом ячейки будем обозначать индексом s , этот индекс принимает l различных значений. Любой атом кристалла однозначно определяется радиус-вектором , задающим положение ячейки (соответствующего узла решетки Браве), и индексом s , характеризующим положение атома внутри ячейки (тип атома).

Смещение атомов при колебаниях решетки является линейной комбинацией плоских гармонических волн (точнее, их вещественных частей): (40).

Частота колебаний одинакова для всех атомов кристалла. Амплитуда колебаний зависит от типа атома (индекса s ), тоесть одинакова для всех однотипных атомов. Направление вектора амплитуды может, вообще говоря, быть каким угодно.

Индекс j обозначает ветвь колебаний. Волновой вектор и ветвь j однозначно определяют частоту и относительные амплитуды атомов всех типов. Для каждой ветви зависимости и являются непрерывными функциями.

Если примитивная ячейка кристалла содержит l атомов, то число ветвей равно 3l . Таким образом, каждому значению волнового вектора соответствуют 3l разных колебаний.

Три из этих ветвей – акустические, в предельном случае длинных волн их частота пропорциональна длине волнового вектора ω = |k |. Однако скорость звука зависит от направления распространения волны, то есть от направления вектора . В случае длинноволновых акустических колебаний амплитуды всех атомов примитивной ячейки примерно одинаковы.

Остальные 3l –3 ветвей – оптические , при их частота отлична от нуля.

По направлению амплитуды относительно волнового вектора акустические колебания можно разделить на продольное и два поперечных. Как правило, скорость звука у продольного колебания больше, чем у поперечных.

У кристаллов со структурой алмаза или цинковой обманки примитивная ячейка содержит 2 атома. Соответственно, кроме трех акустических, эти кристаллы обладают тремя оптическими ветвями колебаний, из которых также можно выделить продольную и две поперечных ветви.

Как и в одномерном случае, волновые вектора, отличающиеся друг от друга на вектор обратной решетки, соответствуют одному и тому же колебанию. По этой причине достаточно рассматривать волновые вектора, лежащие в первой зоне Бриллюэна.

Количество разрешенных волновых векторов в зоне Бриллюэна равно N = V /v ₀ – числу примитивных ячеек в нормировочном объеме кристалла V = L ³ (v ₀ – объем примитивной ячейки). Действительно, плотность разрешенных волновых векторов в обратном пространстве равна V /(2π )³ , т. е. в объеме обратного пространства Δ ³ k содержится Δ ³ k · V /(2π )³ разрешенных волновых векторов. Объем зоны Бриллюэна – объем примитивной ячейки обратной решетки — равен (2π )³ /v ₀ , и для числа разрешенных состояний получаем (2π )³ /v ₀ · V /(2π )³ = V /v ₀ = N .