Курсовая работа: Колебания кристаллической решетки

Обсудим теперь особенности закона дисперсии (12).

Важным его свойством является то, что частота волн, распространяющихся по цепочке, ограничена частотой . Чтобы оценить эту частоту, надо знать порядок величины постоянной γ .

Посмотрим на размерность γ . Сила F равна произведению γ на смещение u , поэтому:

(15).

Характерная длина, межатомное расстояние a , имеет порядок 1A = 10^–8 cм. Характерная энергия – энергия, которую приобретает атом при смещении на расстояние порядка a . Ее можно оценить как энергию химической связи, которая по порядку величины равна 10 эВ. Таким образом:

(16).

В качестве массы для оценки можно подставить величину 10M_p , где M_p ≈ 1,67· 10^–27 кг – масса протона.

Для ω_max получаем:

(17).

Найдем длину волны электромагнитного излучения такой частоты:

(18).

Электромагнитные волны с такой длиной принадлежат инфракрасному диапазону.

При ka /2<<1, когда длина волны λ = 2π /k много больше a , sin(ka /2)≈ ka /2, поэтому:

(19).

Таким образом, длинноволновые колебания – это звуковые волны с линейным законом дисперсии ω = |k |. Выше мы уже получали такой результат, заменив точное уравнение цепочки (2) волновым уравнением (3). Это и неудивительно: длинные волны ''не чувствуют'' дискретной структуры цепочки, цепочка ведет себя как непрерывная упругая среда. По этой причине скорость звука зависит только от макроскопических характеристик цепочки: линейной плотности, M /a , и упругой постоянной цепочки γ a – коэффициента пропорциональности между относительным удлинением цепочки и возникающей при этом силой натяжения:

(20).

Рассмотренные нами колебания одномерной цепочки называют акустическими, поскольку при k → 0 (λ →∞) они соответствуют звуковым волнам.

Ниже мы увидим, что в цепочке с двумя (и более) атомами в элементарной ячейке наряду с акустическими могут распространяться волны другого типа.

При квантовомеханическом описании каждому колебанию соответствует квазичастица с импульсом p = ħ k и энергией . Квазичастицы, соответствующие упругим колебаниям кристаллической решетки называются фононами . Фононы, соответствующие акустическим колебаниям, также называются акустическими.

Оценим максимальную энергию акустического фонона в одномерной цепочке:

(21)

Экспериментальные значения ħω_max в реальных кристаллах составляют 30 ч 40 мэВ.

Эта величина намного меньше большинства характерных электронных энергий (~ 1 эВ) и близка к тепловой энергии при комнатной температуре (kT ≈ 0.025эВ, здесь k – постоянная Больцмана).

1.2.Одномерная цепочка с двумя атомами в примитивной ячейке

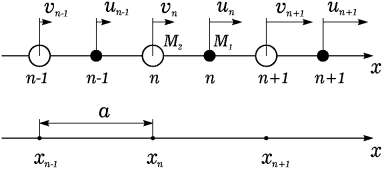
Исследуем теперь колебания цепочки, элементарная ячейка которой состоит из двух атомов с разными массами: M ₁ и M ₂ , для определенности положим M ₁ <M ₂ . Период цепочки (расстояние между узлами ее решетки Браве) как и прежде обозначим через a (рис. 3). Для простоты будем считать, что ''пружинки'' соединяющие атомы имеют одинаковую жесткость γ .

Рис. 1. 3. Одномерная цепочка с двумя атомами в примитивной ячейке и ее решетка Браве.

Запишем закон Ньютона для двух атомов n -й ячейки:

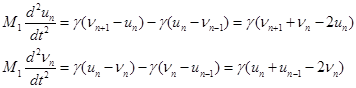(22).

Здесь u_n и v_n – смещения соответственно маленького и большого атома n -й ячейки из положения равновесия.