Курсовая работа: Колебания кристаллической решетки
Введение. 2
Глава 1. Колебания кристаллической решетки. 3
1.1.Одномерная цепочка с одним атомом в ячейке. 4
1.2.Одномерная цепочка с двумя атомами в примитивной ячейке. 11
1.3. Трехмерный кристалл. 13
Глава 2. Фононы. Фононный газ. 16
Глава 3. Акустическая и оптическая ветки колебаний.19
Решение со знаком ''минус''19
Решение со знаком ''плюс''.22
Глава 4. Энергия колебаний и теплоемкость кристаллической решетки. 26
4.1. Модель Эйнштейна. 27
4.2. Модель Дебая. 27
Выводы.. 34
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ.. 35
Введение
Одной из важных и сложных задач теории твердого тела является расчет теплоемкости и теплопроводности твердого тела. Для твердых тел в рамках классической механики были получены значения теплоемкости, которые лишь приблизительно были равны реальным значениям теплоемкости при нормальных температурах. При повышенных температурах и при температурах следующих к абсолютному нулю значения теплоемкости оказались зависимы от температуры, чего классическая теория объяснить не могла. Лишь использование квантовой теории смогло объяснить эту зависимость.
Для нахождения величин теплоемкости и теплопроводности твердых кристаллических тел в широком температурном диапазоне вводят понятие фононов – квазичастиц, которые распространяются в твердом теле.
К данной работе мы рассмотрим явления колебаний кристаллической решетки, которые и являются фононами и их виды в зависимости от строения вещества. Также рассмотрим процессы рассеивания с участием акустических и оптических фононов.
Глава 1. Колебания кристаллической решетки
Кристаллическая структура – равновесное состояние системы атомов, отвечающее минимуму потенциальной энергии. В состоянии покоя сумма сил, действующих на каждый атом кристалла со стороны других атомов, равна нулю.
Если вывести эту систему из положения равновесия, в кристалле возникнут сложные колебания. Эти колебания, в частности, всегда имеются при конечной температуре, когда кристаллическая структура обладает определенной (тепловой) энергией, то есть не находится в состоянии статического равновесия.
Рассмотрим колебания решетки в рамках классической механики.
При смещении атома относительно других атомов кристалла возникает сила, стремящаяся вернуть его в равновесное положение. Если смещения невелики, мы можем разложить зависимость силы от смещений в ряд и ограничится линейными по смещениям членами. Тогда колебания кристаллической решетки будут линейными, то есть будут описываться системой линейных дифференциальных уравнений.
Такая система уравнений обладает важным свойством: если есть несколько решений, то их сумма также является решением и сумма двух возможных колебаний – тоже колебание.
Эта система может быть решена, если известна зависимость силы, действующей на атом, от его смещения, а основные характеристики линейных колебаний могут быть предсказаны на основании одних только свойств симметрии кристалла.
Чтобы показать главные черты линейных колебаний кристаллической решетки, мы рассмотрим простейший случай одномерного кристалла – одномерную цепочку атомов.
1.1 Одномерная цепочка с одним атомом в ячейке
Рассмотрим одномерную периодическую цепочку атомов – одномерный кристалл с одним атомом в элементарной ячейке. Пусть период этой цепочки равен a . Тогда в состоянии равновесия координата n -го атома цепочки xn равна na .
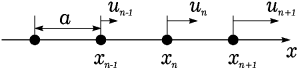
Рис. 1.1. Одномерная цепочка с одним атомом в элементарной ячейке.
Обозначим через un смещение n -го атома из положения равновесия. Будем считать, что атомы взаимодействуют только с ближайшими соседями. Сила, с которой (n +1)–й атом действует на n -й зависит от разности смещений этих двух атомов un +1 –un . При небольших смещениях эту силу можно считать пропорциональной разности смещений: Fn ,n +1 = γ (un +1 –un ), где γ – коэффициент пропорциональности. Удобно представить, что атомы связаны друг с другом пружинками с жесткостью γ .
На рис.1.1 пружинка между n -м и n +1 -м атомами растянута, так что она действует на n -й атом в положительном направлении. Растянутая пружинка между n –1-м и n -м атомом действует на n -й атом в отрицательном направлении: Fn ,n –1 = –γ (xn –xn –1 ).
Запишем закон Ньютона для n -го атома цепочки:
--> ЧИТАТЬ ПОЛНОСТЬЮ <--