Курсовая работа: Линейное и нелинейное программирование
Допустимое базисное оптимальное решение:
X = (2, 4, 7, 0, 0, 5)
F = -14 
2.1.7 Решение двойственной задачи
Прямая задача:

Двойственная задача:
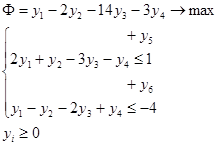
Приводим к каноническому виду:
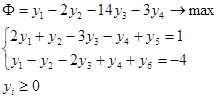
y1 , y3 – базисные переменные, y2 , y4 , y5 , y6 – свободные переменные
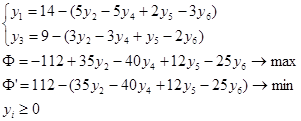
| ↑ | |||||||||
| b | y2 | y4 | y5 | y6 | |||||
| ← | y1 | 14 | 5 | -5 | 2 | -3 | 14/5 | ||
| 14/5 | 1/5 | -1 | 2/5 | -3/5 | |||||
| y3 | 9 | 3 | -3 | 1 | -2 | 3 | |||
| -42/5 | -3/5 | 3 | -6/5 | 9/5 | |||||
| Ԓ | 112 | 35 | -40 | 12 | -25 | ||||
| -98 | -7 | 35 | -14 | 21 | |||||
| b | y2 | y4 | y5 | y6 | |||||
| y1 | 14/5 | 1/5 | -1 | 2/5 | -3/5 | ||||
| y3 | 3/5 | -3/5 | 0 | -1/5 | -1/5 | ||||
| Ԓ | 14 | -7 | -5 | -2 | -4 | ||||
| x1 | x2 | x3 | x4 | x5 | x6 |
| ↕ | ↕ | ↕ | ↕ | ↕ | ↕ |
| y5 | y6 | y1 | y2 | y3 | y4 |
| 2 | 4 | 7 | 0 | 0 | 5 |
F’ = Ф’ = 14
X = (2,4,7,0,0,5)
F= -F’ = -14 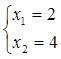
2.2 Задача целочисленного линейного программирования
2.2.1 Постановка задачи целочисленного линейного программирования
Решить ЗЦЛП, при условии целочисленности всех переменных, входящих в задачу, методом ветвей и границ и методом отсекающих плоскостей (методом Гомори).
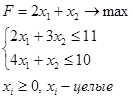
2.2.2 Метод Гомори
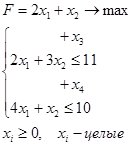
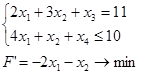
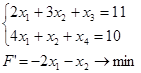
x3 , x4 – базисные переменные, x1 , x2 – свободные переменные
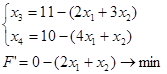
| ↑ | |||||
| b | x1 | x2 | |||
| x3 | 11 | 2 | 3 | 11/2 | |
| -5 | -1/2 | -1/2 | |||
| ← | x4 | 10 | 4 | 1 | 10/4 |
| 5/2 | 1/4 | 1/4 | |||
| F’ | 0 | 2 | 1 | ||
| -5 | -1/2 | -1/2 | |||
| ↑ | |||||
| b | x4 | x2 | |||
| ← | x3 | 6 | -1/2 | 5/2 | 12/5 |
| 12/5 | -1/5 | 2/5 | |||
| x1 | 5/2 | 1/4 | 1/4 | 10 | |
| -3/5 | 1/20 | -1/10 | |||
| F’ | -5 | -1/2 | 1/2 | ||
| -6/5 | 1/10 | -1/5 | |||
| b | x1 | x2 | |||
| x3 | 12/5 | -1/5 | 2/5 | ||
| x4 | 19/10 | 3/10 | -1/10 | ||
| F’ | -31/5 | -2/5 | -1/5 | ||
X = (19/10, 12/5, 0, 0)
F = -F’ = 31/5
Составляем неравенство Гомори:
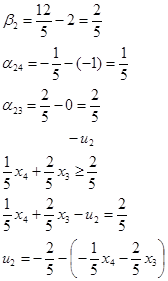
| ↑ | |||||
| b | x4 | x3 | |||
| F’ | -31/5 | -2/5 | -1/5 | ||
| 1/5 | 1/10 | -1/2 | |||
| x2 | 12/5 | -1/5 | 2/5 | ||
| -2/5 | -1/5 | 1 | |||
| x1 | 19/10 | 3/10 | -1/10 | ||
| 1/10 | -1/4 | ||||
| ← | u2 | -2/5 | -1/5 | -2/5 | |
| 1 | 1/2 | -5/2 | |||
| b | x4 | u2 | |||
| F’ | -6 | -3/10 | -1/2 | ||
| x2 | 2 | -2/5 | 1 | ||
| x1 | 2 | 7/20 | -1/4 | ||
| x3 | 1 | 1/2 | -5/2 | ||